Carnoturile Carnot reprezintă o reprezentare grafică a operațiilor de lipire parțială parțială și absorbție elementară.
Carnoturile Carnot sunt tratate ca o tabelă a adevărului rearanjată a funcției.
Carnot Maps este o scanare plat definită a unui cub Boolean n-dimensional.
Tabela de adevăr a funcției este construită într-un anumit mod. Fiecare celulă din tabel corespunde unui vârf complet definit al cubului boolean. Valorile zero nu sunt înregistrate.
Carnot harta pentru o funcție de 4 variabile:
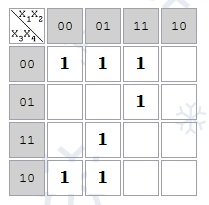
Harta Carnot este privită ca suprafața unei figuri numită torus ("bagel").
celule p - celule ale hărții Carnot care corespund valorii unitare a funcției.
Seturile vecine sunt seturi care diferă doar într-un singur argument (o orbită).
Orice pereche de seturi vecine din Carnot Map corespund celulelor vecine.
Două celule p adiacente de pe harta Carnot dau un implicant al primului rang. De exemplu, celulele 1100 și 1101 diferă numai prin valoarea lui x3. în consecință, ele dau implantul 124.
Doi participanți vecini ai primului rang formează un implicant al celui de-al doilea rang.
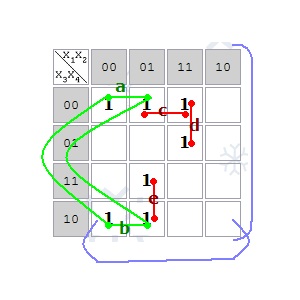
Pe această hartă, celulele vecine formează implicații a, b, c, d, e. În acest caz, implicanții a și b sunt adiacenți, deci formează un implicant al celui de-al doilea rang.
Dacă funcția are 5 variabile, atunci sunt extrase două hărți Carnot: pentru x5 = 0 și pentru x5 = 1. Dacă 6 variabile sunt 4 Hărți, astfel încât celulele învecinate să aibă aceleași coordonate:
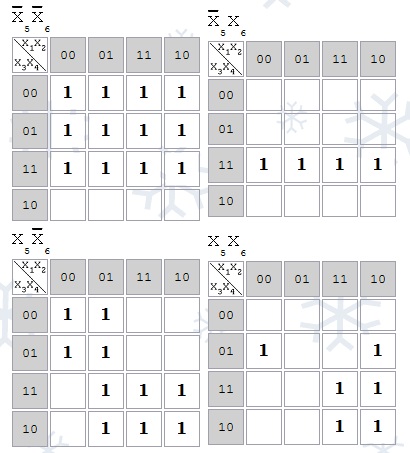
Celulele p-adiacente care corespund grupului implicat formează un grup compact.
Numărul celulelor p într-un grup compact este de două.
Sarcina de a minimiza funcția de comutare cu ajutorul hărților Carnot este de a găsi un implicant de rang superior (corespunzător grupurilor compacte de cea mai mare dimensiune) care să acopere celulele p ale funcției în cel mai bun mod.
Dacă toate grupurile compacte de cea mai mare dimensiune se disting pe hărțile Carnot, atunci disjuncția conjuncțiilor corespunzătoare va da un SCDHF.