Fie ca matricea să fie o cantitate scalară. Deși împărțirea matricei într-o altă matrice nu este definită strict, matricea poate fi întotdeauna divizată într-o cantitate scalară. Această diviziune constă în împărțirea fiecărui element al matricei cu un număr dat.
Matricile sunt obiecte matematice vectoriale care conțin 2 sau mai multe elemente scalare. Matricele sunt folosite pentru a găsi numeroase necunoscute în sistemele de ecuații scalare și pentru operațiunile cu numere mari. Ca și în cazul valorilor scalare (de exemplu, prin numerele 1, 2, 3, 4), cu matrici este posibilă efectuarea unor calcule matematice, cum ar fi adunarea, scăderea și multiplicarea. Cu toate acestea, matricile nu pot fi împărțite în mod direct unul în celălalt. Pentru a diviza matricile, este necesar să se efectueze o acțiune constând din două etape. Mai întâi se determină matricea, care este inversa divizorului (numitor). Apoi, pe această matrice, se multiplică pe cea împărțită sau pe matricea-numărător. Această metodă vă permite să obțineți rezultatul dorit fără a face o divizare directă. Acest articol descrie modul de divizare a matricelor.
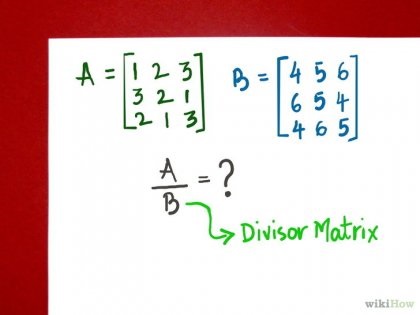
Determinați matricea inversă la matricea numitorului. Metode pentru găsirea matrici inverse și a altor operații cu matrici pot fi găsite în manuale și cărți de referință de matematică. Calculați determinantul matricei numitorului. Procedura de identificare a determinantului matricei este descrisă în manualele matematice. Scopul acestei etape este de a determina dacă determinantul matricei este diferit de zero. Dacă determinantul matricei-divizor este zero, aceasta înseamnă că matricea este ireversibilă, adică nu există pentru matricea inversă. În acest caz, întrerupeți orice altă acțiune. Dacă matricea inversă a matricei divizoare nu există, atunci nu putem continua. O astfel de situație este similară cu împărțirea la zero, nepermisă pentru cantitățile scalare. Dacă determinantul nu este zero, găsiți matricea inversă la matricea numitorului. Cele mai comune modalități de a găsi matricea inversă - metoda lui Gauss-Jordan și procedura de constatare a matricei de cofactori. Verificați dacă ați găsit matricea inversă corect. Înmulțiți matricea inversă cu o linie dreaptă, ca rezultat ar trebui să obțineți o matrice unitate. O matrice unitară este una a cărei elemente sunt zero, cu excepția diagonalei, care este egală cu una.
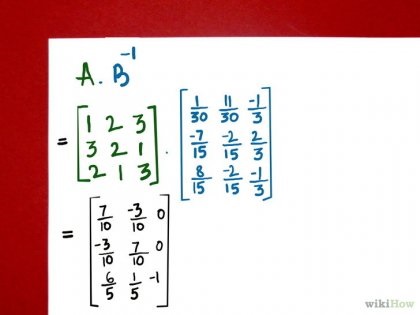
Înmulțiți matricea-numărător cu matricea numitorului invers. Rețineți că, spre deosebire de multiplicarea cantităților scalare, în acest caz ordinea multiplicatorilor este semnificativă. Când numerele multiplicatoare 2, înmulțit cu 4 dă același rezultat ca și cel al 4 înmulțit cu 2. în vectorul matrice numărătorului multiplicare matematică prin matricea numitorul inverse dă un rezultat diferit de cel în cazul în care o matrice inversă este multiplicat cu o matrice numărător.
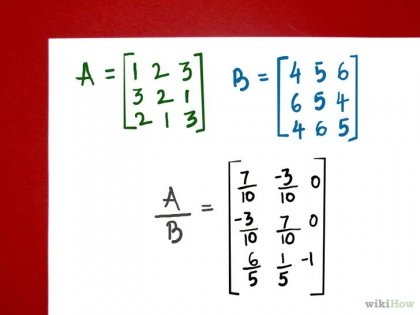
Rețineți că rezultatul înmulțirii matricelor corespunde cu cel dorit. O matrice care nu este definită strict într-o algebră matricială se calculează prin găsirea matricei inverse și înmulțirea matricei divizibile cu ea.
254310 254311 254312