În această lucrare sunt luate în considerare principiile de calcul al grinzilor de rezistență inegală la momentul de încovoiere. astfel de grinzi de secțiune dreptunghiulară, unul dintre parametrii geometrici ai secțiunii transversale scade invers proporțional cu momentul de îndoire a acțiunii. Principiile de bază pentru calcularea acestor grinzi sunt aceleași ca și pentru grinzile cu rezistență egală la momentul de încovoiere, dar există unele caracteristici.
1. Calculul grinzilor de secțiune transversală dreptunghiulară, variația unuia dintre parametrii geometrici ai secțiunii transversale inversate, se poate realiza pe baza următoarelor ipoteze:
1.1. Deoarece nici unul dintre parametrii geometrici, de exemplu, lățimea grinzilor articulate variază de la b la începutul deschiderii la 0 la mijlocul deschiderii nu este (o astfel de fascicul este distrus), acesta calculează mai întâi puterea și pe baza acestui calcul sunt determinate de parametrii geometrici ai mai încărcate secțiune. Prin urmare, această grindă poate fi considerată ca două grinzi: una cu o lățime constantă și o a doua lățime care variază de la δb la 0. Diagrama momentului pentru caracteristica de deviere a fasciculului de secțiune transversală constantă, și, în plus, această epure poate fi considerată ca epure normală tensiuni de curent continuu pentru grinzi secțiune.
1.2. Diagrama generală a tensiunilor normale care apar în secțiunile transversale ale fasciculului caracterizează deformarea generală a fasciculului.
1.3 Dacă impunem o diagramă de moment pe diagrama de tensiune a unui fascicul cu secțiune variabilă variabilă, urmărind anumite condiții, diferența dintre aceste diagrame va arăta schimbarea deflecției pentru un fascicul de secțiune variabilă.
Mai exact diferența dintre domeniile acestor diagrame pot fi privite ca un fel de sarcină fals și apoi diferența dintre aceste diagrame indică schimbarea suportului dummy de reacție A, o valoare obținută prin împărțirea rigidității - schimba unghiul de rotire pe suport A. Apoi, punct fictiv (reacție de susținere inactiv, înmulțită cu distanța față de punctul de aplicare a reacției lagărului manechinului la punctul în cauză, minus pătratul diagramelor de diferență, înmulțită cu distanța față de centrul de greutate al diagramei diferență față de punctul în cauză) arată variația deflexie.
Notă. sunt luate în considerare principiile metodei grafice-analitice din acest articol.
De exemplu, pentru un fascicul cu o lățime variabilă liniar b, diagrama diferențială va arăta astfel:
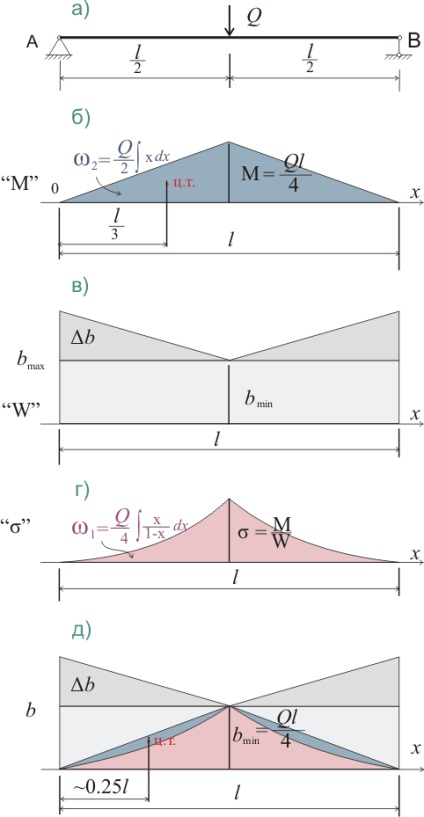
În acest caz, diagrama diferențială va fi afectată nu numai de natura încărcării pe grindă, ci și de abaterea de la dimensiunea minimă permisă a secțiunii transversale. Deci, dacă δb → 0, atunci secțiunea transversală a fasciculului tinde la o valoare constantă. Cu o creștere semnificativă în δb în comparație cu b, eficiența utilizării materialelor scade, deși deformarea scade. Condiția δb → b nu este permisă de constrângerile de la §1.1. Prin urmare, calcularea grinzilor cu o secțiune transversală descrescătoare de la începutul fasciculului până la mijloc depinde de valoarea lui bmin. În plus, natura schimbării tensiunilor normale depinde de valorile bmin și δb.
Deformarea unui fascicul cu o lățime liniară descrescătoare a unei secțiuni cu o sarcină concentrată în mijlocul intervalului
1.4. Deoarece schimbarea tensiunilor normale pentru un fascicul cu o sarcină concentrată este descrisă de o dependență a formei:
atunci pentru o valoare constantă h 2/6 = C = 1 formula (323.1.1) are forma:
După transformările corespunzătoare, obținem următoarea relație:
În cazul în care bmin în cazul unei constante și valoarea acesteia poate fi luată egală cu 1. Apoi, de exemplu, atunci când δb = bmin = b / 2, n = 2, y = 2, o curbă diferență este descrisă prin două linii având următoarea relație:
În acest caz, valoarea reacției de referință A = Q / 2 este o valoare constantă, iar pentru simplificarea calculelor se poate lua în afara limitelor de integrare. Aceste linii se intersectează la punctele 0 și 0.5 (începutul fasciculului și mijlocul intervalului sau limita inferioară și superioară a integrării), apoi:
atunci aria diagramei diferențiale va fi:
Notă. În acest caz, suntem interesați de diagrama diferențială deoarece este mult mai ușor să determinăm distanța față de centrul de greutate al diagramei diferențiale decât să căutăm centrul de greutate al diagramei cu aria ω1. Din punct de vedere vizual (Fig.323.1 e), această distanță este l / 4. În plus, graficele funcțiilor au fost reprezentate pentru evaluarea vizuală a rezultatelor integrării pentru diagramele de torsiune și tensiune din Figurile 323.1 - 323.3 (vezi Fig.323.1.2).
Valoarea momentului de încovoiere fictiv este:
Mt = Ql 2/16 (l / 3) - (0.22712Ql 2/16) (l / 4) = Ql 3/48 - 3/48 0.17Ql = 0.83Ql 3/48 (323.2.5)
În acest caz, Ibmin înseamnă că avem în vedere schimbarea deflecției în raport cu fasciculul cu un moment constant de inerție și, în consecință, o lățime constantă bmin în secțiune transversală.
Pentru a face din ce în ce mai evident, pentru cazul în cauză o creștere a materialului fasciculului cu un factor de 1,5 conduce la o reducere a deformării cu 1,184 de ori.
Dacă schimbarea lățimii secțiunii este descrisă de o altă relație, atunci rezultatele aproximative pot fi obținute prin interpolarea datelor din Figura 323.1.2.
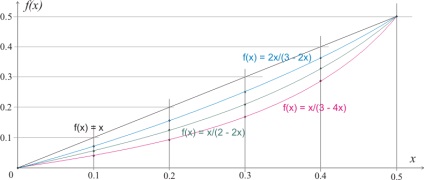
După cum se vede din această figură, când raportul δb / b = 1/3 (f (x) = 2x / (3 - 2x)) pătrat diferență diagramă va fi de aproximativ 2 ori mai mică decât atunci când se analizează un raport de 1/2. La un raport de 2/3, suprafața diagramei diferențiale va crește cu aproximativ 1/2.
Deformarea unui fascicul cu o lățime liniară descrescătoare a unei secțiuni cu o sarcină uniform distribuită
Cu o sarcină uniform distribuită, atât diagrama de moment, cât și schema normală de tensiune
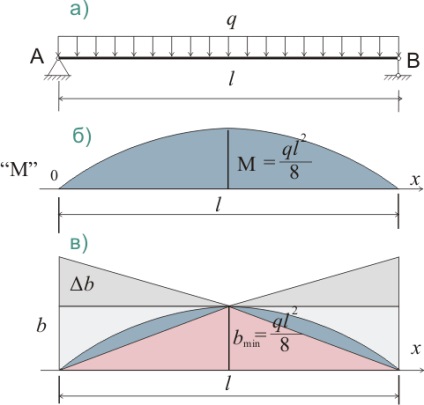
σ = M / W = 6 (qlx - qx2) / 2bh2 (323.4.1)
atunci pentru o valoare constantă de h 2/3 = C = 1 formula 323.1.1) ia forma:
Pentru bmin = 1, pentru δb = bmin = b / 2, n = 2, y = 2x, diagrama diferențială este descrisă de două linii având următoarea relație:
Aceste linii se intersectează la punctele 0 și 0.5 (începutul fasciculului și mijlocul intervalului sau limita inferioară și superioară a integrării), apoi:
atunci aria diagramei diferențiale va fi:
Apoi, valoarea momentului de îndoire fictiv este:
Mt = ql 3/24 (5l / 16) - (ql 3/96) (l / 4) = 5QL 4/384 - ql 4/384 = ql 4/96 = 4ql 4/384 (323.4.8)
În acest caz, Ibmin înseamnă, de asemenea, că avem în vedere schimbarea în deflecție în raport cu fasciculul cu un moment constant de inerție și, prin urmare, o lățime constantă a secțiunii transversale bmin.
Pentru a face din ce în ce mai evident, cu o încărcătură distribuită uniform, creșterea factorului de fascicol cu un factor de 1,5 duce la o reducere a deviației cu un factor de 1,2.
Dacă lungimea fasciculului este luată și ca unitate, admisă pentru limitele de integrare alese de noi, ecuațiile funcțiilor vor arăta astfel:
Ie în acest caz graficul care descrie diagrama de tensiune are o dependență liniară (figura 323.2b).
Deformarea unui fascicul cu o înălțime liniară descrescătoare, cu o sarcină concentrată în mijlocul fasciculului
Din momentul rezistentei W = bh 2/6 pentru o secțiune dreptunghiulară, chiar dacă înălțimea relației descrescătoare liniar între stres și de moment diagrame normale nu liniar chiar și atunci când sarcina concentrată aplicată fasciculului la jumătatea distanței. Cu o sarcină uniform distribuită, definiția deflecției prin metoda de integrare devine și mai complicată. Dar, în general, efectul elevație modificări asupra schimbării deflexie, deoarece în acest caz nu ar trebui luate în considerare pentru a modifica înălțimea și piața de înălțimi diferite, precum și momentul de inerție este I = bh 3/12 pentru o secțiune transversală dreptunghiulară, diagrama moment, ar trebui să fie comparată cu o schimbare cubică înălțimea secțiunii.
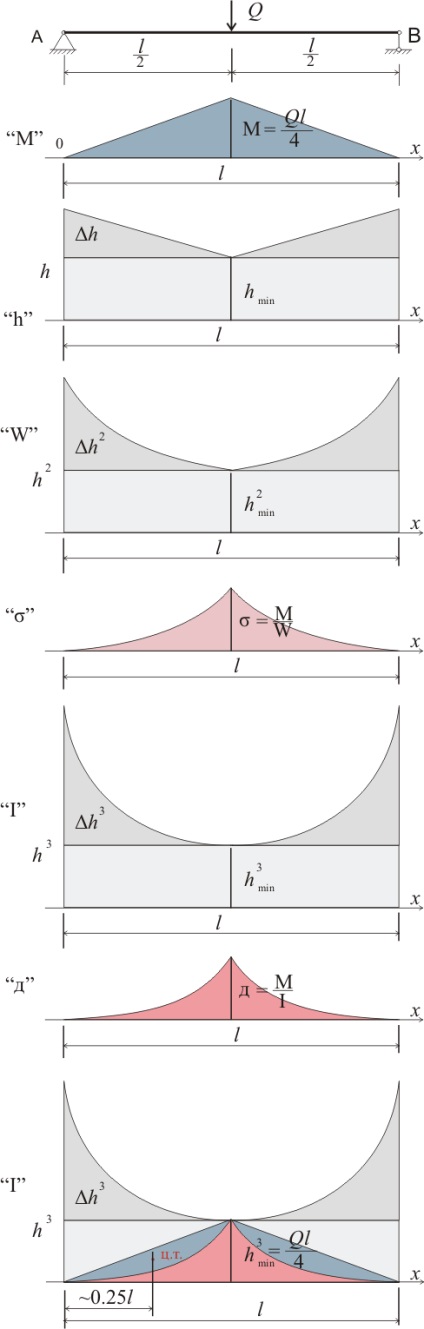
Atunci când δh = hmin = h / 2, n = 2, y = 2x, diagrama diferențială este descrisă de două linii având următoarea relație:
atunci aria diagramei diferențiale va fi:
Valoarea momentului de încovoiere fictiv este:
Mt = Ql 2/16 (l / 3) - Ql 2/32 (l / 4) = Ql 3/48 - Ql 3/128 = (1 - 0.375) Ql 3/48 = 0.625Ql 3/48 (323,5. 5)
Notă. Distanța de la centrul de greutate al diagramei diferențiale la origine este determinată vizual conform figura 323.3.
Deformarea unui fascicul cu o înălțime a secțiunii descrescătoare liniar, cu o sarcină uniform distribuită
Deoarece scăderea liniar lățimea secțiunii din diferența jgheaburi atunci când sarcina concentrată aplicată în mijlocul deschiderii și o sarcină distribuită uniform este extrem de scăzut, putem presupune că același lucru va fi o mică diferență și variază liniar înălțimea secțiunii transversale. Apoi, pentru δh = hmin = h / 2
Deformarea unui fascicul cu o înălțime a secțiunii descrescătoare proporțional cu momentul de încovoiere
Un exemplu de astfel de fascicul este orice grinzã de beton armat suspendat, cu fisuri în zona întinsã. Ca urmare a acțiunii tensiunilor normale, înălțimea secțiunii comprimate a secțiunii fasciculului se modifică neliniar. Această relație poate fi exprimată aproximativ după cum urmează:
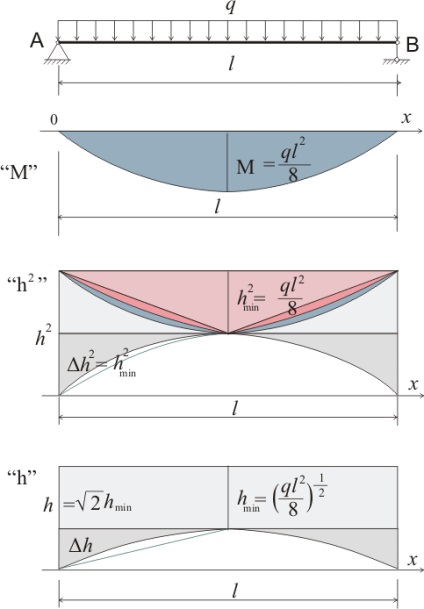
Grinzile de beton armat cu armare în zona întinsă pot fi considerate ca o rază de secțiune variabilă. În secțiuni transversale, în care momentul de încovoiere este zero sau foarte mică, tensiunea de compresiune provocând deformarea elastică a betonului, solicitări de tracțiune provoacă o deformare elastică și beton și armătură. La schema de design ales compresibil este partea de sus a secțiunii, și întinse partea inferioară a secțiunii. După ce tensiunea a atins limita de rezistența la întindere a betonului la intindere, beton in zona alungibil incepe sa se descompuna - va forma fisuri - și, prin urmare, cu creșterea rezistenței la întindere tot mai mare parte a acestor tensiuni va percepe toate valvele și partea mai mică partea inferioară a secțiunii de beton. Astfel, înălțimea secțiunii reduse a fasciculului va scădea. Înălțimea minimă a secțiunii reduse va fi în punctul de acțiune al momentului maxim de îndoire.
În acest caz, o creștere a momentului de încovoiere va conduce la o scădere a înălțimii pătratului ariei secțiunii comprimate (diagrama "h 2"). Diagrama "h 2" prezintă, de asemenea, efectul unei modificări neliniare în înălțimea secțiunii transversale în comparație cu o schimbare liniară a înălțimii secțiunii transversale. Cu o astfel de schimbare neliniară în înălțime, aria diagramei diferențiale cu raportul hmin = h / 2 va fi de 2 ori mai mică decât pentru o schimbare liniară a altitudinii.
Dacă luăm în considerare numai deformările elastice ale regiunii comprimate a secțiunilor de beton, atunci o scădere a pătratului înălțimii de două ori înseamnă o schimbare a înălțimii δh de la 0 la hmin / √2.
Astfel, folosind datele obținute prin analizarea fasciculelor cu o lățime și înălțime liniară descrescătoare a secțiunii transversale, efectul total al schimbării neliniare în înălțime și modificarea raportului hmin / h poate fi exprimat ca:
FPR ≈ 5QL 4 / 384EIhmin - 2ql 4 /(384·2·1.41EIhmin) = (5 - 0,7) ql 4 / 384EIhmin ≈ 4.3ql 4 / 384EIhmin ≈ 0,86 · 5QL 4 / 384EIhmin (323.7.6.1)
În acest caz, valoarea 0.86 poate fi considerată ca fiind valoarea factorului de corecție, luând în considerare înălțimea variabilă a fasciculului.
Notă. O determinare mai precisă a efectului modificării înălțimii secțiunii transversale a zonei comprimate pe deformarea este sarcina destul de consumatoare de timp, în special, trebuie remarcat faptul că înălțimea secțiunii nu va începe să se schimbe imediat de la începutul fasciculului cât mai aproape de poli la o schemă de design dat va fi zonele fără fisuri. Dar, chiar dacă, în cursul greșelilor de raționament au fost făcute, este încă valoarea exactă a coeficientului nu poate depăși 0,8-0,9, deoarece estimările pentru deformarea grinzi din beton armat sub o sarcină distribuită uniform poate fi utilizat în formula de mai sus (323.7.6) valoarea. Cu toate acestea, determinarea devierii grinzilor din beton armat cu mult mai mare impact poate avea deformări plastice în zona comprimată de beton și ca o consecință - reducerea modulului inițial de elasticitate a betonului la o anumită secțiune a lungimii fasciculului care poate fi văzută ca o nouă reducere a înălțimii secțiunii transversale.
În consecință, dacă din orice motiv schimbarea înălțimii secțiunii transversale este h / 2, atunci
FPR ≈ 5QL 4 / 384EIhmin - 2ql 4 / (2 · 384 · EIhmin) = (5 - 1) ql 4 / 384EIhmin ≈ 4ql 4 / 384EIhmin ≈ 0,8 · 5QL 4 / 384EIhmin (323.7.6.2)
Dacă schimbarea înălțimii este de la 0 la hmin / 2√ 2. atunci
FPR ≈ 5QL 4 / 384EIhmin - 2ql 4 /(384·2·2·1.41EIhmin) = (5 - 0.35) ql 4 / 384EIhmin ≈ 4.65ql 4 / 384EIhmin ≈ 0,93 · 5QL 4 / 384EIhmin (323.7.6.3)