Viteza unghiulară este notată cu litera greacă omega (w), indicând unghiul la care corpul se rotește pe unitate de timp. Aceasta este magnitudinea arcului în măsura gradului pe care corpul o trece de-a lungul unei perioade de timp. Observați că, dacă solidul se rotește, atunci viteza unghiulară pentru orice puncte de pe acest corp va fi constantă. Mai aproape de punctul este spre centrul de rotație sau mai departe - nu este important, adică nu depinde de rază.
Unitatea de măsură în acest caz va fi fie un grad pe secundă, fie un radian pe secundă. Adesea cuvântul "radian" nu este scris, dar este scris cu -1. De exemplu, găsim ceea ce este egal cu viteza unghiulară a pământului. Pământul face o întoarcere completă la 360 ° în 24 de ore, iar în acest caz se poate spune că viteza unghiulară este.
De asemenea, rețineți relația dintre viteza unghiulară și viteza liniară:
Trebuie remarcat faptul că mișcarea de-a lungul cercului la o viteză constantă este un caz particular de mișcare. Cu toate acestea, mișcarea de-a lungul circumferinței poate fi inegală. Viteza se poate schimba nu numai în direcție și rămâne aceeași în modul, dar și variază în sens, adică Pe lângă schimbarea direcției, există și o modificare a modulului de viteză. În acest caz vorbim despre așa-numita mișcare accelerată de-a lungul cercului.
Subiect: Legile de interacțiune și mișcarea corpurilor
Lecția 22. Rezolvarea problemelor
Yuryutkin Evgeny Sergheițich
Lecția se referă la rezolvarea problemelor
Problema 1 este dedicată legii gravitației universale.
Stare: determinați înălțimea la care forța de gravitație va fi de 3 ori mai mică decât pe suprafața Pământului.
Având în vedere: SI Soluția:
h -. Răspuns: h »4685 km.
În condiția în care se afirmă că gravitatea trebuie să fie de 3 ori mai mică decât pe suprafața Pământului. Forța F1 este forța de atracție a corpului față de Pământ pe suprafața Pământului și forța F2 la o anumită înălțime.
Întrucât problema se referă la legea gravitației universale. Să scriem această lege, dar o vom face de două ori. Prima dată - pentru un corp care se află pe suprafața Pământului și pentru a doua oară - pentru un corp care se află la o anumită înălțime relativ la suprafața Pământului. Deci, F1 este forța gravitației, sau forța gravitației corpului, masa pe care m-am făcut-o Pământului însuși. Legea în sine va fi scrisă după cum urmează :.
Acum scriem formula forței F2. care corespunde forței de interacțiune dintre un mic corp m și masa pământului, corpul masei Pământului la o anumită înălțime h :.
Se știe din condiția că F1 și F2 sunt legate de:. Acum combinăm aceste două ecuații într-un sistem și împărțim ecuațiile între ele.
Pentru a face următorul pas, trebuie să extrageți rădăcina pătrată din părțile din dreapta și din stânga.
Răspunsul final este obținut în formula care determină înălțimea :.
Dacă înlocuim acum toate valorile cunoscute, obținem răspunsul: h »4685 km.
Această problemă arată în mod clar posibilitatea de a determina altitudinea la care poate fi lansat un satelit în așa fel încât o anumită valoare gravitațională să acționeze asupra acestuia. Aceasta este o condiție importantă pentru studierea mișcării sateliților.
Problema 2 este dedicată mișcării curbilinii.
Starea: Ciclista se deplasează de-a lungul curbei drumului, raza curburii drumului este de 50 m, viteza bicicletei este de 36 km / h. Determinați accelerația centripetală a ciclistului care trece prin rotunjirea drumului și determinați forța de frecare care acționează asupra bicicletei.
Având în vedere: SI Soluția:
Găsiți AC necesar și forța de frecare care acționează asupra ciclistului. Pentru a face acest lucru, în primul rând, 36 km / h vor fi transferate în sistemul SI - 10 m / s. Să ne îndreptăm spre soluție. Amintiți-vă că accelerația centripetală este definită ca raportul dintre pătratul vitezei și raza curbei drumului :.
În acest caz, puteți scrie.
Aceasta este accelerația centripetală. Acum putem spune, deoarece avem o accelerare centripetală, adică există o forță îndreptată spre centrul cercului, ceea ce înseamnă că o altă forță acționează ca o contrabalansare, deoarece corpul se deplasează de-a lungul unui cerc de rază constantă, fără alunecare și alunecare. Aceasta este forța de frecare dintre roți și drum. În acest caz, trebuie să rețineți că FTP = Fc. Conform celei de-a doua legi a lui Newton, FTR = Fc = m. AC. Deci, FTR = 60. 2 = 120 H. Răspuns: aC = 2 m / s 2 și FTR = 120 H.
Rețineți că, dacă forța de frecare și forța centripetă nu au fost egale, atunci ne-ar fi văzut un derapaj sau o bicicletă care se rotește rotunjirii, s-ar rupe echilibrul.
Deci, trecem la cea de-a treia problemă finală, care va fi dedicată mișcării rectilinii.
Starea: determinarea vitezei inițiale a corpului, care, deplasându-se vertical în sus, la 2 secunde după începerea mișcării, a atins o viteză de 5 m / s. Determinați înălțimea la care va fi corpul atunci când viteza sa devine 5 m / s.
h -. Răspuns: h = 30 m.
Să începem cu viteza inițială. Uite, vom scrie mai întâi ecuația completă a vitezei. . Amintiți-vă că accelerarea scăderii libere în rezolvarea problemelor, vom lua egal. Acum avem nevoie de un cadru de referință.
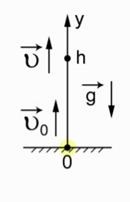
Fig. 1. Sistemul de referință ales pentru a rezolva problema
Sistemul de referință este conectat la suprafața Pământului. Acum ecuația, ecuația de viteză cu cadrul de referință selectat este compatibilă. Notați, în ceea ce privește acest cadru de referință, viteza inițială este direcționată vertical în sus, coincisând cu direcția axei y.
Viteza în 2 secunde, care este definită ca 5 m / s, este de asemenea direcționată vertical în sus. Accelerarea caderii libere este îndreptată vertical în jos. Aici am indicat această accelerare prin săgeata indicată. Mai jos scriem ecuația: V = V0 - g. T. Substituind valorile cunoscute, avem: 5 = V0 - 10. 2.
Din aceasta rezultă că viteza inițială, adică Viteza cu care corpul este aruncat vertical în sus va fi. Astfel, folosind ecuația vitezei și cadrul de referință, am determinat viteza inițială. Următorul pas este de a determina înălțimea.
Vom scrie ecuația mișcării într-o formă generală :.
Am spus deja că viteza inițială este direcționată vertical în sus, va fi cu un semn plus. Accelerația căderii libere este direcționată în raport cu axa în jos și va avea un semn minus. În acest caz, obținem înălțimea, lungimea deplasării de-a lungul liniei drepte este. Răspunsul este egal cu h = 30 m.
Răspuns: h = 30 m.