Matematicienii greci s-au angajat în principal în geometrie și au petrecut mult timp numărând numărul de puncte situate pe plan în formă de figuri geometrice diferite. Numărul de puncte care alcătuiesc
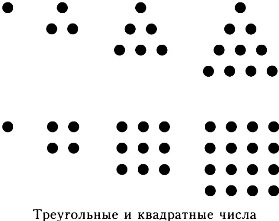
Se poate imagina un triunghi supermicroscopic format dintr-un punct. Trei puncte formează de asemenea un triunghi, care are două puncte pe fiecare parte. Șase puncte formează un triunghi deja mai mare, care are trei puncte pe fiecare parte și zece puncte - un triunghi, care are patru puncte pe fiecare parte.
Puteți scrie numere triunghiulare într-un rând: 1, 3, 6, 10, 15, 21. 28, 36, 45, 55 și așa mai departe. Fiecare următor număr triunghiular formează un triunghi, care are încă un punct pe fiecare parte. Un număr de numere triunghiulare poate fi continuat pe o perioadă nedeterminată.
Rețineți că un număr de numere triunghiulare formează o relație definită. Primul număr este 1, următorul este 3, adică 1 + 2, apoi merge 6, adică 1 + 2 + 3, apoi 10, adică 1 + 2 + 3 + 4, apoi 15, + 4 + 5 și așa mai departe. Amintiți-vă de această dependență, puteți continua un număr de numere triunghiulare atât cât doriți, fără a crea triunghiuri sau puncte de relatare. Pentru a determina dacă un anumit număr este triunghiular sau nu, este posibil prin prezentarea acestuia sub forma unei serii similare cu cea dată mai sus. Dacă numărul poate fi reprezentat ca o sumă de numere, în care fiecare număr următor este mai mult decât numărul precedent, iar primul număr este o unitate, atunci acest număr este triunghiular.
Orice grup de numere care pot fi reprezentate ca o secvență care respectă unele reguli formează o serie numerică.
Numerele, care reprezintă numărul de puncte din care puteți face un pătrat, pot fi de asemenea reprezentate ca o serie. Ca și în ultima oară, un punct poate fi considerat o pereche super-microscopică
Puteți scrie numere quadrangulare într-un rând: 1, 9, 16, 25, 36, 49 și așa mai departe. Fiecare număr patrulater următor formează un patrulater, pe care pe fiecare parte există un alt punct. Un număr de quadrangles poate fi continuat pe o perioadă nedeterminată.
Analizând numerele care alcătuiesc o serie de numere quadrangulare, vom vedea că și ei sunt supuși unei anumite dependențe. Să începem cu 1. Nu există opțiuni, o unitate este doar o unitate. Dar deja 4 = 1 + 3, apoi 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7 și așa mai departe.
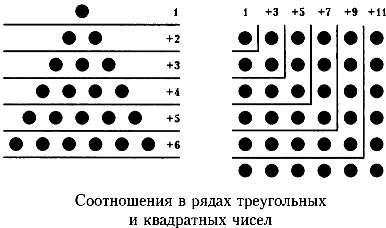
Relația dintre numerele de rânduri triunghiulare și patrate este prezentată în diagramă.
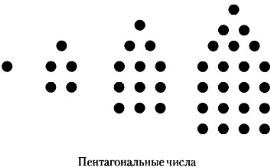
Grecii aveau de asemenea numere pentagonale. care sunt prezentate în figură. Această serie poate fi privită ca un fel de sinteză a seriilor triunghiulare și quadrangulare. Dacă construim mai multe pentagoane în același mod în care am construit triunghiuri și patrulaterale, obținem o serie numerică a formelor 1, 5, 12, 22, 35, 51, 70 și așa mai departe. Aceasta este o serie de numere care se obțin prin adăugarea de numere care diferă una de alta cu trei. Primul membru al seriei este o unitate. Al doilea - 5, adică 1 + (1 + 3) = 1 + 4. Al treilea este 12, adică 1 + 4 + (4 + 3) = 1 + 4 + 7, al patrulea este 22, adică 1 + 4 + 7 + 10 și așa mai departe.
Grecii au inventat și alte figuri geometrice. modelarea seriilor numerice. Numerele care alcătuiesc astfel de secvențe sunt numite figurative. Unele cifre nu se mai modelează prin figuri plate, ca un triunghi și un pătrat, ci prin figuri tridimensionale, cum ar fi cuburile. Astfel de cuburi sunt greu de imaginat în figură, dar dacă vă uitați atent la seria numerică, veți putea să vă faceți o idee despre figura cubică a punctelor. O serie de numere cubice este o serie de 1, 8, 27, 64, 125 și așa mai departe.
Un număr de cifre cubice reprezintă, de asemenea, o serie de sume de numere impare. Cu toate acestea, aceste sume nu încep cu unitatea. Primul membru al seriei este 1, al doilea este 8 sau 3 + 5; a treia este de 27 sau 7 + 9 + 11; a patra este de 64 sau 13 + 15 + 17 + 19. Fiecare grup de numere care urmează să fie însumat începe cu un număr impar de cel care a completat suma anterioară, iar numărul de termeni din fiecare sumă următoare este unul mai mult decât cel precedent.
Materiale pe tema:
Trimiteți-le prietenilor: