Secțiunea 3. EQUACAȚII LINEARE ȘI SISTEMELE LOR
24. Soluția problemelor prin intermediul ecuațiilor liniare. Ecuația ca model matematic al problemei
Am considerat deja exemple de relații funcționale între cantități ca modele matematice ale proceselor reale. Acum, luați în considerare problemele de text, ale căror modele matematice sunt ecuații liniare și ecuații care se reduc la cele liniare.
Rezolvați problema cu ajutorul ecuației în următoarea secvență:
1) desemnează o variabilă ca fiind una dintre cantitățile necunoscute;
2) alte cantități necunoscute (dacă există) pot fi exprimate în funcție de variabila introdusă:
3) prin condiția problemei, stabilirea relației dintre necunoscute și valorile cunoscute ale cantităților și formarea ecuației;
4) rezolva ecuația rezultată;
5) analizați soluția ecuației și găsiți cantitatea necunoscută și, dacă este necesar, și valorile cantităților necunoscute rămase;
6) scrieți răspunsul la sarcină.
Considerăm câteva probleme și le rezolvăm folosind o ecuație liniară.
Sarcina 1. În ziua de naștere, sora gemenei Natalia și Elena au primit împreună 127 de mesaje de întâmpinare prin SMS, iar Natalia a primit 13 mesaje mai mult decât Elena. Câte SMS-uri au primit fiecare dintre surorile ei pentru ziua ei de naștere?
Soluții. Lăsați Elena să primească x mesaje, apoi Natalia - (x + 13). Și ambele împreună - (x + x + 13) mesaje, care după condiție este egală cu 127.
Avem ecuația x + x + 13 = 127. De unde x = 57.
Astfel, Elena a primit 57 de mesaje,
57 + 13 = 70 (comunicat) - Natalia a primit.
În viitor: 70 de mesaje; 57 de mesaje.
Sarcina 2. Valoarea maximă posibilă a creditului este calculată de către bancă conform formulei:
unde S este suma creditului, C este salariul mediu lunar al debitorului. Pentru perioada de creditare de un an, se consideră că n = 9, timp de doi ani - n = 21, pentru o perioadă de trei ani - n = 33. Care ar trebui să fie cel mai mic salariu mediu al debitorului, banca l-a scăzut de credit în valoare de 30 000 UAH pe:
Razv 'z a zanny. Prin condiția S = 30 000 UAH. Să salariul cel mai mic lunar mediu al debitorului este x UAH.
1) Avem următoarea ecuație: 30 000 = ∙ 9; de unde x = 10.000.
În consecință, salariul mediu lunar al debitorului trebuie să fie de cel puțin 10 000 UAH.
2) Avem următoarea ecuație: 30 000 = ∙ 21; unde x ≈ 4285,7.
În consecință, salariul mediu lunar ar trebui să fie de cel puțin 4286 UAH.
3) Avem următoarea ecuație: 30 000 = ∙ 33; unde x ≈ 2727.3.
Deci, în cazul în care un împrumutat vrea să obțină un împrumut timp de trei ani, atunci salariul mediu lunar ar trebui să fie de cel puțin 2728 UAH.
În viitor: 1) 10 000 UAH; 2) 4286 UAH; 3) 2728 UAH.
Sarcina 3. De la orașul A la orașul V. Distanța dintre ele este de 310 km, un camion stâng. 30 de minute mai târziu, o mașină de pasageri a plecat din orașul B spre orașul A, a cărui viteză este cu 20 km / h mai mare decât viteza camionului. Masinile se intalnesc in 2 ore dupa plecarea din masina. Găsiți viteza fiecărei mașini.
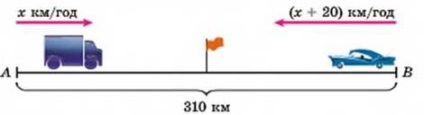
Razv 'z a zanny. Lăsați viteza camionului - x km / h. Starea problemei este prezentată în mod convenabil sub forma unui tabel:
Pe masura ce autovehiculele au condus in directii opuse si s-au intalnit, atunci impreuna au condus 310 km.
Avem ecuația: 2, 5x + 2 (x + 20) = 310.
Să o rezolvăm: 2,5 x + 2х + 40 = 310; 4,5 = 270;
х = 60 (km / h) - viteza utilajului de transport uzinal;
60 + 20 - 80 (km / h) - viteza automobilului.
Răspuns: 60 km / h; 80 km / h.
Ce ordine ar trebui urmată la rezolvarea problemei utilizând ecuația?
892. (Oral) Un număr este de 20 mai mult decât cel de-al doilea. Cel mai mic dintre ele este notat cu x. Exprimați prin x cel mai mare dintre aceste numere.
893. (Oral) Un număr pozitiv este de 5 ori mai mare pentru al doilea. Cel mai mic dintre ele este notat cu x. Exprimați prin x cel mai mare dintre aceste numere.
894. Într-o singură grădină crește x tufișuri de trandafiri, iar pe a doua - de două ori mai multe. Exprimați prin x numărul de tufișuri de trandafir care cresc pe cea de-a doua grădină de flori.
895. (Oral) Distanța, egală cu x km, ciclistul depășește în 5 ore. Exprimați viteza mișcării sale prin x.
896. (Oral) Primul număr este notat cu x, iar al doilea este un sfert de la primul. Exprimați al doilea număr în termeni de x.
897. Primul număr este x. 70% din cele dintâi. Exprimați al doilea număr în x.
898. (Oral) Suma lungimilor a două segmente este egală cu 10 cm. Lungimea unuia dintre celelalte este: Exprimați lungimea celui de-al doilea segment prin x.
899. (Oral) Viteza proprie a barcii este de 18 km / h, iar viteza curentului este de x km / h. Exprimați prin x viteza barcii de-a lungul curentului și împotriva curentului.
900. Ghiciți numărul. Dacă luăm 7 ori mai departe de el și împărțim rezultatul cu 9, atunci ajungem la 12. Ce număr au făcut?
901. Găsiți numărul jumătate dintre acestea, împreună cu a treia parte, este de 40.
902. În două tancuri împreună 58 de tone de combustibil, iar în primele 4 tone mai puțin decât în cel de-al doilea. Câte tone de combustibil în fiecare rezervor?
903. În flota de camioane există de 6 ori mai mult decât autoturismele. Câte mașini din flotă, dacă sunt împreună cu încărcătura 91?
904. Unul dintre numerele pozitive este de trei ori mai mare decât al doilea. Găsiți aceste numere dacă diferența lor este de 28.
905. Bunicile și mama au 99 de ani. Cât de veche este fiecare dintre ei, dacă bunica este mai veche decât mama ei timp de 25 de ani?
906. Suma a două numere este 360, iar raportul lor este 5. 7. Găsiți aceste numere.
907. Diferența dintre cele două numere este de 42, iar raportul lor este 7. 4. Găsiți aceste numere.
908. Perimetrul triunghiului este de 20 dm. Cele doua laturi sunt egale unul cu altul si fiecare dintre ele este de 1 dm mai mare decat al treilea. Găsiți laturile triunghiului.
909. De două zile, au fost vândute 384 kg de banane, iar a doua zi a fost vândută pentru că au vândut primul. Câte kilograme de banane au fost vândute în prima zi și cât de mult în al doilea?
910. Turiștii pentru a doua zi au depășit de la acea distanță care au depășit prima zi. Cati kilometri au depasit turistii in prima zi si cate secunde, daca prima zi a fost depasita cu 3 km mai mult decat cea de-a doua?
911. Pentru masina de spalat si conexiunea sa a fost platit 2940 UAH. Costul de conectare este de 5% din costul mașinii. Cât costă o mașină de spălat?
912. Bunica facea vareniki timp de două ore. Pentru cea de-a doua oră, ea a turnat 5% mai mult vareniki decât prima. Cât de multe vareniki făcute de bunica pentru prima oră și cât de mult pentru a doua, dacă pentru a doua oră a modelat 3 vareniki mai mult decât prima?
913. Timp de 2 ore, motociclistul depășește aceeași distanță cu ciclistul în 5 ore. Viteza motociclistului este cu 27 km / h mai mare decât viteza ciclistului. Găsiți viteza fiecăruia.
914. O cutie de portocale de 3 kg mai greu decât o cutie de lămâi. Care este masa fiecăruia, dacă masa a patru cutii cu portocale este aceeași cu greutatea a cinci cutii cu lămâi?
915. Din oraș până în sat turistul a mers la o viteză de 4 km / h și a revenit la o viteză de 3 km / oră. Tot așa a petrecut 7 ore. Găsiți distanța de la oraș la sat.
916. Perimetrul dreptunghiului este de 36 cm, iar una din laturile sale este de 4 cm mai mare decât celălalt. Găsiți laturile dreptunghiului și a zonei acestuia.
918. Masha avea de trei ori mai mulți bani decât Olya. După ce Masha a petrecut 18 UAH, banii fetelor au devenit egali. Cati bani au avut la inceput fiecare fata?
919. Rețeaua de cofetării până la aniversarea deschiderii sale a dat vizitatorilor dulciuri de seturi de mărci "Bine", "Dulce" și "Delicioase". La sfârșitul sărbătorii, sa arătat că "Dulce" a fost prezentat cu 12 seturi mai mult decât trusele "Bune", iar seturile "Delicious" - 31 mai mult decât &всехuo;E dulce. Câte seturi de fiecare brand a fost dat, dacă vizitatorii au fost 430 și fiecare dintre ei a primit un set?
920. O latură a triunghiului este de 9 cm mai mică decât a doua și jumătate a celei de-a treia. Găsiți laturile triunghiului dacă perimetrul său este de 105 cm.
921. Pot să descompun 68 de cutii de conserve în trei cutii, astfel încât în cel de-al doilea să fie de două ori mai multe cutii ca în primul și în al treilea - 3 cutii mai mici decât în primul?
922. Sau pot fi plasate 90 de cărți pe trei rafturi, astfel încât al treilea să aibă 3 cărți mai mult decât al doilea și 5 cărți mai puțin decât primul?
923. Tatăl meu are acum 38 de ani, iar fiul său este 10. Câți ani va fi tatăl de trei ori mai bătrân decât fiul său?
924. Pe un singur loc de tufișuri de coacăze și de trei ori mai mult decât pe a doua. Dacă de la primul loc pentru a transplanta 12 tufișuri pe a doua, apoi Bush de coacăze pe ambele site-uri vor fi împărțite în mod egal. Câte tufișuri de agrișă cresc pe fiecare loc?
925. În două clădiri ale pensiunii a trăit același număr de turiști. În legătură cu reparația, sa hotărât resetarea a 24 de turiști de la prima clădire la a doua, după care numărul turiștilor din prima clădire a fost de 4 ori mai mic decât în cel de-al doilea. Cât de mulți turiști au locuit în fiecare clădire înainte de începerea lucrărilor de reparații?
926. În două saci de zahăr erau cincizeci și cincizeci. După ce primul sac a fost turnat la 8 kg în al doilea, a fost jumătate cât mai mult zahăr decât în al doilea. Cati kilograme de zahar au fost in fiecare sac in primul rand?
927. Pentru 33 de grivne au fost achiziționate 24 de notebook-uri în linie și celulă. Costul unui notebook în gama este de 1 UAH 20 copeici. și în caseta - 1 UAH 50 copeici. Câte notebook-uri de fiecare tip au cumpărat?
929. O sarcină antică greacă. Pitagora a fost întrebat: "Câți elevi studiază la școala ta?". La care a răspuns: "Jumătate dintre studenții mei studiază matematica, un sfert - muzică, a șaptea parte este tăcută și, în plus, există și alte trei femei". Câți elevi au studiat la școala Pitagora?
930. Greutatea unei cutii de lapte este de 25 kg, iar jumătate din greutatea sa. Care este masa recipientului cu lapte?
931. de la un număr este egal - de la al doilea. Găsiți aceste numere dacă suma lor este 66.
932. 60% din un număr este egal cu 45% din cel de-al doilea. Găsiți aceste numere dacă suma lor este 210.
933. Barca a petrecut 2,5 ore pe drum și 3,6 ore împotriva curentului. Distanța pe care barca a înflorit de-a lungul curentului a fost de 7,6 km mai mică decât distanța pe care o învârtea împotriva curentului. Găsiți propria viteză a vaporului dacă viteza curentului este de 2 km / h.
934. Barca de-a lungul râului a curg 1,6 ore, iar împotriva curentului - 2,5 ore. Distanța pe care barca a traversat-o împotriva curentului sa dovedit a fi de 6,2 km mai mare decât distanța pe care barca a trecut-o de-a lungul curentului. Găsiți viteza curentă dacă viteza proprie a vaporului este de 16 km / h.
935. Un ciclist a plecat de la punctul A la punctul B la o viteză de 12 km / h. După 3 ore, un motociclist a plecat la punctul B de la punctul A cu o viteză de 45 km / h. Câte ore înainte de întâlnirea cu motociclistul a fost ciclistul, dacă distanța de la A la B este de 235,5 km? Cât de departe de punctul A s-au întâlnit?
936. Un ciclist a părăsit cabana în direcția gării la o viteză de 14 km / h, iar după două ore un pieton a ieșit de acolo, dar în direcția opusă la o viteză de 4 km / h. Câte ore după ieșirea sa, pietonul se va afla la o distanță de 73 km de ciclist? La ce distanță de cabana în acest moment va fi localizată?
937. Un pepene verde este de 5 kg mai ușor decât cel de-al doilea și de trei ori mai ușor decât cel de-al treilea. Primul și al treilea pepene verde sunt de două ori mai grele decât cel de-al doilea. Găsiți masa fiecărui pepene verde.
938. În timpul pregătirii pentru olimpiada de matematică, Ivan a decis trei sarcini mai puțin decât Oksana și de două ori mai puțin decât Serghei. În același timp, Ivan și Serghei împreună au dezlănțuit de 2,1 ori mai multe sarcini decât Oksana. Câte sarcini le-a rezolvat fiecare elev, pregătindu-se pentru olimpiada?
Exerciții pentru repetare
5. Sau sunt ecuațiile echivalente 3x - 2 = x + 8 și 2 (x - 3) = x - 1?
6. Într-un coș au fost două ori mai multe ciuperci ca în al doilea. Câte ciuperci erau în fiecare coș, dacă în ambele coșuri existau 78 de ciuperci împreună?
2) 5x - (x + 5) = 4 (x - 2).
8. Barca a mers în aval de 3,5 ore, iar față de curent - 4,2 ore. Distanța pe care barca a înflorit-o de-a lungul curentului a fost de 9,8 km mai lungă decât distanța pe care o învârtea împotriva curentului. Găsiți propria viteză a vaporului dacă viteza curentului este de 2 km / h.
9. Găsiți toate valorile întregi ale unui a pentru care rădăcina ecuației ax = -6 este un număr întreg.
10. Rezolvați ecuația | 3-4x | = 5.
11. De la oraș la sat s-a dus un pieton cu o viteză de 4 km / h. Două ore mai târziu un ciclist cu o viteză de 16 km / h a părăsit satul în oraș. Câte ore înainte de întâlnirea cu pietonul a fost ciclistul, dacă distanța de la sat până la oraș este de 38 km?