Prezentare pe tema: "Puncte geometrice de puncte Punctul geometric al punctelor (HMT) este o cifră care constă din toate punctele care satisfac o anumită proprietate sau mai multe." - Transcriere:
Puncte geometrice de puncte Un loc geometric de puncte (HMT) este o cifră care constă din toate punctele care satisfac o anumită proprietate sau mai multe proprietăți specificate. Exemple de puncte geometrice ale punctelor sunt: cerc - HMT, îndepărtat de la un punct dat la o anumită distanță; cerc - HMT, îndepărtat de la acest punct la o distanță care nu depășește aceasta.

2 Exercițiul 1 Marcați punctele situate la nodurile grilajului și distanțate de punctul O cu o distanță egală cu 2. (laturile celulelor sunt egale cu 1). răspundă:
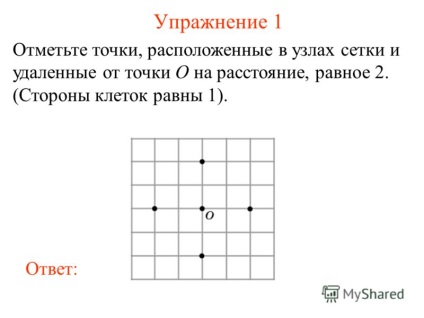
3 Exercițiul 2 Marcați punctele situate la nodurile rețelei și distanțate de punctul O cu o distanță mai mică de 2. (laturile celulelor sunt egale cu 1). răspundă:
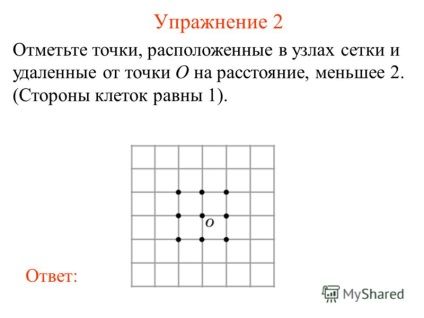
4 Exercitarea 3 Marcați punctele situate la nodurile rețelei și distanțate de punctul O cu o distanță mai mare de 2 și mai mică de 3. (laturile celulelor sunt egale cu 1). răspundă:
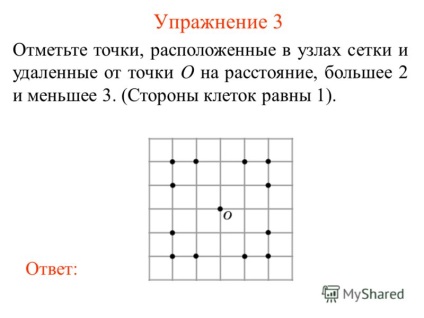
5 Exercitarea 4 Marcați punctele situate la nodurile rețelei ale căror distanțe față de punctele A și B sunt mai mici de trei. (Laturile celulei sunt egale cu 1). răspundă:
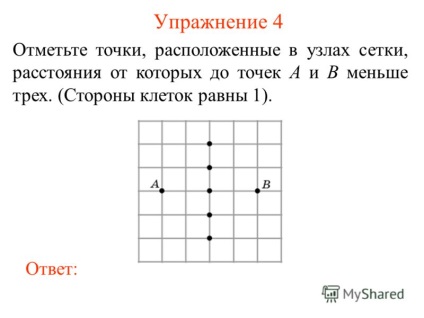
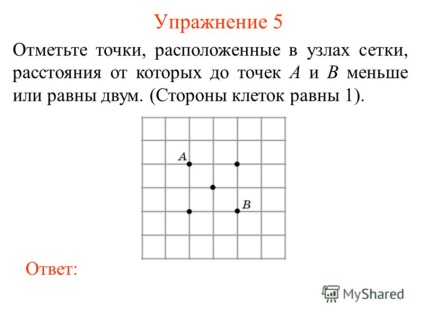
6 Exercitarea 5 Marcați punctele din nodurile rețelei ale căror distanțe față de punctele A și B sunt mai mici sau egale cu două. (Laturile celulei sunt egale cu 1). răspundă:
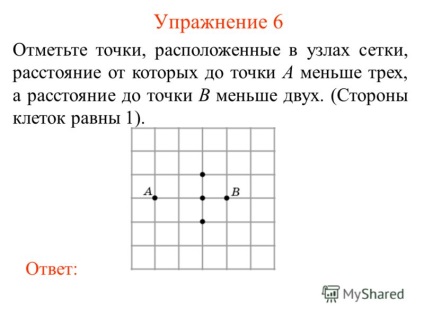
7 Exercitarea 6 Marcați punctele situate în nodurile rețelei, distanța de la care la punctul A este mai mică de trei, iar distanța până la punctul B este mai mică de două. (Laturile celulei sunt egale cu 1). răspundă:
8 Exercitarea 7 Marcați punctele situate în punctele de rețea, distanța de la care la punctul A este mai mare de două, iar distanța până la punctul B este mai mică de două. (Laturile celulei sunt egale cu 1). răspundă:

9 Exercitarea 8 Marcați punctele situate la punctele de rețea, distanța de la care la punctul A este mai mică decât distanța până la punctul B, iar distanța până la punctul B este mai mică decât distanța până la punctul C. Răspuns:

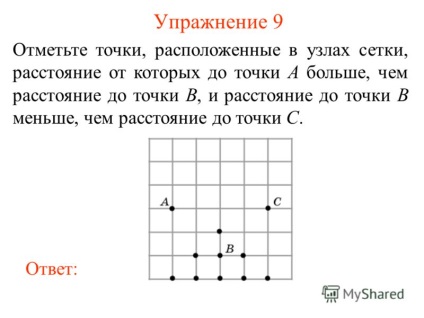
10 Exercitarea 9 Marcați punctele situate la punctele de rețea, distanța de la care la punctul A este mai mare decât distanța până la punctul B, iar distanța până la punctul B este mai mică decât distanța până la punctul C. Răspuns:
11 Exercitarea 10 Marcați punctele situate în nodurile rețelei, din care segmentul AB este vizibil la un unghi de 90 °. răspundă:

12 Exercitarea 11 Marcați punctele de la punctele din rețea, din care segmentul AB este vizibil la un unghi de 90 °. răspundă:
13 Exercitarea 12 Marcați punctele situate în nodurile rețelei, din care segmentul AB este vizibil la un unghi de 90 °. răspundă:
14 Exercitarea 13 Marcați punctele situate în punctele de rețea, din care segmentul AB este vizibil la un unghi de 45 °. răspundă:
15 Exercitarea 14 Marcați punctele situate în nodurile rețelei, din care segmentul AB este vizibil la un unghi de 45 °. răspundă:
16 Exercitarea 15 Marcați punctele situate în nodurile rețelei, din care segmentul AB este vizibil la un unghi de 135 °. răspundă:
Teorema mediană perpendiculară. Mijlocul perpendicular pe segment este HMT, la fel de îndepărtat de capetele acestui segment. Mijlocul perpendicular pe segment este o linie dreaptă perpendiculară pe acest segment și care trece prin mijlocul său. Dovada. Fie ca segmentul AB să fie dat și punctul O să fie punctul său central. Evident, punctul O este la fel de îndepărtat de punctele A, B și aparține perpendicularului mediu. În schimb, permiteți-vă ca punctul C să aparțină perpendicularului mediu și să nu coincidă cu O, atunci triunghiurile drepte AOC și BOC sunt egale (prin picioare). În consecință, AC = BC. Fie punctul C la fel de îndepărtat de punctele A și B și nu coincide cu punctul 0. Apoi, triunghiul ABC este isoscele și C0 este media. Prin proprietatea unui triunghi isoscel, mediana este și înălțimea. Aceasta înseamnă că punctul C aparține perpendicularului mediu.
18 Exercițiul 1 Desenați un HMT echidistant de la punctele A și B. Răspuns:
19 Exercițiul 2 Pe linia c, desenați un punct C echidistant față de punctele A și B. Răspuns:
20 Exercitarea 3 Desenați un HMT echidistant de la punctele A și B. Răspuns:
21 Exercițiul 4 Pe linia c, desenați un punct C echidistant față de punctele A și B. Răspuns:
22 Exercițiul 5 Desenați un HMT echidistant de la punctele A și B. Răspuns:
23 Exercițiul 6 Pe linia c, desenați un punct C echidistant față de punctele A și B. Răspuns:
24 Exercitarea 7 Marcați un punct echidistant de la punctele A, B și C. Răspuns:
25 Exercitarea 8 Marcați un punct echidistant de la punctele A, B și C. Răspuns:
26 Exercitarea 9 Marcați un punct echidistant de la punctele A, B și C. Răspuns:
27 Exercițiul 10 Desenați un loc geometric al centrelor cercurilor care trec prin aceste două puncte. Răspuns: Mediul perpendicular pe segmentul care leagă cele două puncte date.
28 Exercitarea 11 Desenați poziția geometrică a vârfurilor C ale unui triunghi isoscel cu o bază AB dată. Răspuns: Mediul perpendicular pe segmentul AB fără mijlocul acestui segment.
Exercitarea 12 Fie A și B puncte ale planului. Specificați locusul punctelor C, pentru care AC AS. Răspuns: jumătatea planului, definită de mijlocul perpendicular pe segmentul AB, care conține punctul A.
Exercițiul 13 Fie A și B puncte ale unui plan, în linie. Specificați locusul punctelor liniei drepte c, situat mai aproape de A decât de B. În ce caz nu există astfel de puncte? A: O parte din c directe, care se află în interiorul jumătate de planul definit de perpendiculara pe segmentul AB și punctul A. Dacă linia c se află în întregime în semiplanul definit de perpendiculara și punctul B, atunci nu există astfel de puncte.
31 Bisectorul teoremei unghiului. Bisectorul unghiular este un HMT care se află în acest colț și la fel de îndepărtat de laturile sale. Dacă CA = CB, atunci triunghiurile dreptunghiulare AOC și BOC sunt egale (pe hypotenuse și picior). În consecință, unghiurile AOC și BOC sunt egale. Aceasta înseamnă că punctul C aparține bisectorului unghiului. În schimb, dacă punctul C aparține bisectorului unghiului, atunci triunghiurile AOC și BOC cu unghi drept sunt egale (prin hipotenuse și unghi ascuțit). Prin urmare, AC = BC. Prin urmare, punctul C este la fel de îndepărtat de laturile unui anumit unghi. Dovada. Luați în considerare unghiul c cu vârful la punctul O și laturile a, b. Lăsați punctul C să se afle într-un unghi dat. Părăsim din acesta perpendiculele CA și CB pe laturile a și b.
32 Exercitarea 1 Desenați poziția geometrică a punctelor interioare ale unghiului AOB, echidistant față de laturile sale. răspundă:
33 Exercițiul 2 Pe linia c, marcați punctul C echidistant față de laturile unghiului AOB. răspundă:
34 Exercitarea 3 Desenați poziția geometrică a punctelor interioare ale unghiului AOB, echidistant față de laturile sale. răspundă:
35 Exercițiul 4 Pe linia c, marcați punctul C echidistant față de laturile unghiului AOB. răspundă:
36 Exercițiul 5 Desenați poziția geometrică a punctelor interioare ale unghiului AOB, echidistant față de laturile sale. răspundă:
37 Exercițiul 6 Pe linia c, marcați punctul C echidistant față de laturile unghiului AOB. răspundă:
38 Exercitiul 7 Care este locusul geometric al centrelor cercurilor tangente la doua linii intersectate? Răspuns: Bisectoarele unghiurilor formate atunci când aceste linii se intersectează, fără punctul de intersecție al acestor linii.
39 Exercițiul 8 Răspuns: a) Punctele aparținând bisectoarelor celor patru unghiuri formate de aceste linii; b) interioarele a două unghiuri verticale formate din bisectrice. Fie a și b două linii intersectante. Găsiți locusul punctelor: a) la fel de îndepărtat de a și b; b) situat mai aproape de a decât b.
40 Exercițiul 9 Pe linia c care intersectează laturile colțului, găsiți punctul C, la fel de îndepărtat de aceste laturi. Răspuns: Punctul de intersecție al unei linii date cu bisectorul unui unghi dat.
41 Exercitarea 10 Având un unghi AOB și punctele M, N pe laturile sale. În interiorul colțului, găsiți un punct care este la fel de îndepărtat de punctele M și N și se află la aceeași distanță de laturile colțului. Răspuns: punctul de intersecție al mijlocului perpendicular pe MN cu bisectorul unghiului.
42 Intersecția figurilor Fie Φ 1 și Φ 2 figuri în plan. Figura Φ, constând din toate punctele care aparțin figurii Φ 1 și figura Φ 2, se numește intersecția dintre figurile Φ 1 și Φ 2 și este notată cu Φ 1 Φ 2.
43 Exercițiul 1 Răspuns: GMT-ul dorit este intersecția a două cercuri cu centrele la O 1, O 2 și razele R 1, R 2. Sunt date două puncte O 1 și O 2. Gasiți GMT X pentru care XO 1 R 1 și XO 2 R 2. Intersecția dintre care cifrele este GMT dorit.
44 Exercițiul 2 Sunt date două puncte A și B. Găsiți HMT C pentru care CA CB AB. Intersecția dintre care cifre este GMT dorit. Răspuns: GMT-ul dorit este intersecția unui cerc și a unei jumătăți de plan.
45 Exercițiul 3 Sunt oferite trei puncte A, B, C. Găsiți HMT X pentru care AX BX și BX CX. Intersecția dintre care cifre este GMT dorit. Răspuns: GMT-ul dorit este intersecția a două jumătăți de spații definite de perpendiculele medii către segmentele AB și BC.
46 Combinarea figurilor Fie Φ 1 și Φ 2 figuri în plan. Figura Φ, constând din toate punctele care aparțin figura Φ 1 sau figura Φ 2, se numește unirea cifrelor Φ 1 și Φ 2 și este notată cu Φ 1 Φ 2.
47 Exercițiul 1 Se dau două puncte O 1 și O 2. Găsiți HMT X pentru care XO 1 R 1 sau XO 2 R 2. Combinați ce cifre este HMT dorit. Răspuns: HMT căutat este unirea a două cercuri cu centrele în punctele O 1, O 2 și razele R 1, R 2.
48 Exercițiul 2 Sunt date trei puncte A, B, C. Găsiți HMT X pentru care AX BX sau BX CX. Combinația dintre aceste cifre este GMT dorit. Răspuns: HMT căutat este unirea a două jumătăți de spații definite de perpendiculele medii către segmentele AB și BC.
49 Diferența dintre figuri Fie Φ 1 și Φ 2 figuri în plan. Figura Φ, constând din toate punctele care aparțin figurului Φ 1 și care nu aparține figurii Φ 2, se numește diferența dintre cifrele Φ 1 și Φ 2 și este notată cu Φ 1 Φ 2.
50 Exercițiul 1 Răspuns: GMT-ul dorit este diferența a două cercuri cu centrele în punctele O 1, O 2 și razele R 1, R 2. Sunt date două puncte O 1 și O 2. Gasiți GMT X pentru care XO 1 R 1 și XO 2 R 2. Diferența dintre care cifrele este HMT dorit.