180. Astfel, dacă avem 2 segmente y și x, atunci putem forma o ecuație care leagă aceste două segmente în formă (§ 168)
y / x = k sau y = kx,
unde k este un număr rațional sau irațional.
Să luăm acum a doua formă a acestei ecuații, adică y = kx.
Luăm segmentul x pentru unitate, adică, setăm x = 1; atunci din ecuația precedentă obținem y = k, adică dacă segmentul x este estimat de numărul 1, atunci segmentul y este exprimat prin numărul k. Prin urmare, ecuația y = kx este înțeleasă după cum urmează:
Am măsurat segmentul y, luând ca unitate segmentul x, iar ca rezultat al acestei măsurători am obținut numărul k.
1) Lungimea camerei = 8 ½ arshin,
adică am măsurat un segment rectiliniu numit "lungimea camerei", luând un segment numit "arshin" pe unitate, și ca rezultat am obținut numărul 8 ½.
2) Înălțimea acestui om este de 13/16 sazhens,
adică, am măsurat un segment rectiliniu care exprimă creșterea acestei persoane, luând pentru o unitate sazhen, și a primit un număr de 13/16.
3) Segmentul A = 0,377 al segmentului B,
adică, am măsurat segmentul A, luând segmentul B ca unitate și am obținut un număr de 0,377.
Segmentul care este luat ca unitate este numit unitatea liniară: în primul exemplu, unitatea liniară este arshin, în al doilea rând sazhen, în al treilea segment B.
Trebuie remarcat că toate egalitățile precedente pot fi date într-o altă formă:
1) lungimea camerei / arshin = 8½;
2) creșterea acestei persoane / sazhen = 13/16;
3) segmentul A / segmentul B = 0,377,
adică "raportul dintre lungimea camerei și arsin = numărul 8½", raportul dintre creșterea acestei persoane și cea a sazhen = 13/16 "," raportul dintre segmentul A și segmentul B = numărul de 0,377 ".
Astfel, problema "măsurării segmentului A, luând segmentul B ca unitate", coincide cu problema "găsirii raportului dintre segmentul A și segmentul B".
181. Orice două segmente y și x pot fi conectate prin ecuație
unde k este orice număr întreg, fracționar sau irațional. Cu alte cuvinte: fiecare segment poate fi măsurat prin luarea unui alt segment ca o unitate liniară și, ca rezultat al măsurării, se obține un număr întreg, fracțional sau irațional.
În cazul în care numărul de k ar fi rațional (întregi sau fracționare), cele anterioare ecuația y = kx ne va arăta cum putem de la unitatea liniară x obține intervalul măsurat y (de ex. În cazul în care y = 3/7 x, este necesar să se împartă unitatea x liniar pentru y în 7 părți egale și să ia 3 astfel de părți).
În cazul în care numărul de k ar fi irațional, atunci ecuația y = astfel de instrucțiuni KX, nu putem da: deoarece pentru noi irațional și definit doar ca raportul dintre cele două segmente de linie incomensurabile (168 p.). În cazuri excepționale, este posibil ca acest număr irațional să fie exprimat de un alt simbol, de exemplu. √2; atunci această circumstanță ne poate ajuta să obținem un segment y, efectuând unele construcții pe segmentul x.
Prin urmare, se utilizează o măsurătoare aproximativă. În pp. 170 și 172, am învățat să cunoaștem valoarea aproximativă a raportului dintre două segmente:. În Sec 170 suntem în acest scop a folosit capacitatea de a diviza un segment în părți egale, în secțiunea 172 au făcut fără această abilitate, care, cu toate acestea, la punctul 170, putem găsi aproximativă .. cu orice precizie precizată, iar în § 172 am arătat că acest lucru ar fi posibil numai dacă cunoaștem teoria fracțiunilor continue.
Acum va trebui să ne întoarcem la § 170 pentru a interpreta într-o altă formă rezultatele obținute acolo.
Reluați negrul. 185 și pune problema: măsurați segmentul AB cu 1/5, luând CD-ul segment într-o unitate liniară și vom presupune că AB și CD-ul sunt incomensurabile. Am obținut în secțiunea 170 două segmente AK și AL, care sunt ambele comestibile cu unitatea liniară CD, cu AK = 8/5 CD și AL = 9/5 CD. Din moment ce AK
8/5 CD Uneori același lucru este scris în forma: AB = aprox. 8/5 CD (nu este disponibil) sau 9/5 CD (cc). [Explicație. Dacă în locul segmentului AB luăm segmentul AK = 8/5 CD, atunci ceva "lipsește" în comparație cu segmentul AB; prin urmare, scriem în paranteze "cu un defect". Dacă în loc de AB luăm segmentul AL = 9/5 CD, atunci există un "exces" în comparație cu segmentul AB; așa că scriem "în exces" în paranteze.] Având în vedere segmentul AB egal cu 8/5 CD sau 9/5 CD, în ambele cazuri facem o eroare mai mică de 1/5 din CD. Prin urmare, spunem că am măsurat segmentul AB la 1/5 din unitatea liniară CD. Ar fi de asemenea posibil să se măsoare cu precizie segmentul AB printr-o unitate CD liniară cu o precizie de 1/10 CD. De exemplu. ar putea primi 17/10 CD sau AB = aprox. 17/10 CD (nu este disponibil) sau 18/10 CD (cu redundanță). 17/10 182. Putem rezolva problema anterioară într-un mod general: măsurați segmentul AB printr-un CD cu unitate liniară cu o precizie de 1 / n CD. Să divizăm CD-ul (articolul 193) în n părți egale și să punem aceste părți pe AB; lasă-i să satisfacă m cu restul KB și KB <1/n CD (всегда можно дойти до такой точки K — в этом состоит аксиома Архимеда. Отрезок AK = m/n CD, но он меньше отрезка AB, причем разность этих отрезков меньше 1/n CD; Поэтому мы можем принять, что AB = aprox. m / n CD (nu este disponibil). Dacă punctul K amâne încă o dată n-lea parte a unității CD, care se mișcă dincolo de punctul B și un segment obține = (m + 1) / n CD, care este mai mare decât segmentul AB și un segment mai mic de 1 / n CD. Prin urmare, avem din nou: AB = aprox. (m + 1) / n CD (redundant). Același lucru poate fi scris sub forma unor inegalități: m / n CD Observăm că în practică folosim metoda de măsurare aproximativă prezentată aici pentru orice segmente, fără a lua în considerare întrebarea dacă intervalul cunoscut cu unitate liniară este comensurabil sau nu. 183. La punctul 172, găsirea unor valori aproximative, relațiile dintre segmentele AB și CD (186) fără capacitatea de a diviza segmentul în părți egale, am scris: AB = (aprox.) 19/5 CD, adică aici am măsurat aproximativ segmentul AB de unitatea liniară CD, deși nu am știut cu ce exact acest lucru a fost făcut. Ar trebui, totuși, să acorde o atenție la alin. 172, din care se poate observa că pentru măsurarea o lungime a celuilalt, sau pentru a găsi raportul dintre două segmente, capacitatea de a împărți un segment în părți egale, nu este la fel de necesar, deoarece s-ar putea părea la prima vedere. 184. Privind la paragrafe 165 și 172, putem afla proprietățile segmentelor care sunt necesare pentru a găsi raportul dintre două segmente sau, cu alte cuvinte, pentru a strânge segmentele prin numere, luând un anumit segment pe unitate. Este în primul rând capacitatea necesară de a întârzia un segment la altul, și trebuie să poată discerne unde un segment este diferit sau mai mare decât cealaltă sau, în cele din urmă, este mai mică decât alta (pentru că tot timpul p. 165 și p. 172 a trebuit să amâne pentru părțile un segment egal un alt segment, iar pe reziduul rezultat, se stabilește că acesta este mai mic decât segmentul întârziat). Apoi am avut, de exemplu, în 165, să scriem egalități ca sau, în detaliu: Putem scrie astfel de ecuații numai dacă știm ce înseamnă să adăugăm două segmente. Deci, trebuie să știm încă ce înseamnă să adăugăm două segmente și trebuie stabilit că putem găsi suma a două segmente. Toate cunoștințele despre segmente sunt enumerate la începutul cursului de geometrie. Întrucât, după trecerea pp. 165 și 172, vom vedea că nu mai este nevoie de alte cunoștințe despre segmente, atunci putem constata că informațiile date în pp. 8-10, segmentele sunt suficiente pentru capacitatea de a găsi raportul oricărei perechi de segmente. Abilitatea de a împărți segmentul în părți egale, pe care le-am folosit în subsecțiunea 182, este neimportantă, după cum se poate observa din subsecțiunea 172. Dacă aveți o colecție de obiecte, și 1) pentru fiecare două elemente ale acestui set, puteți stabili dacă acestea sunt egale sau unul dintre ele mai mari decât celălalt, și 2) puteți seta conceptul de suma celor două elemente ale acestui set (și, în consecință, diferența lor) * , atunci ei spun că acest set de obiecte poate fi privit ca un sistem de cantități. (* Orice două subiecte din această colecție trebuie să aibă o sumă.) Setul de segmente rectilinie poate fi considerat un sistem de cantități. Fiecare segment individual reprezintă valoarea acestui sistem de cantități. Fiecare valoare a unui sistem de cantități poate fi exprimată printr-un număr, luând valoarea sa diferită definită pe unitate (fiecare segment de linie dreaptă poate fi exprimat printr-un număr, luând o anumită lungime pentru o unitate). Proprietățile segmentelor rectilinie, care permit ca agregatul lor să fie considerate cantități sistemice, sunt exprimate prin cuvintele: fiecare segment rectiliniu are o lungime. În practică, pentru măsurarea segmentelor, se utilizează unitățile selectate o dată pentru totdeauna, numite unități liniare. Iată cele mai comune unități liniare: sazhen, arshin, verst, verst, foot, inch, metru, kilometru, centimetru. În practică, nu se face nici o distincție între, comparabile indiferent dacă sunt sau nu segmentul cu unități, și măsura întotdeauna cu care orice precizie. De exemplu, în cazul în care segmentul redactat pe hârtie, atunci aceasta este aplicată o linie pe care depozitate, de exemplu, inci, împărțit în 10 părți egale fiecare, și vizionarea ca inches întregi și zecimi de inci este plasat pe segmentul dat, ignorând restul este mai puțin de jumătate de o zecime din inch, sau numărați-l pentru o zecime de inch dacă este mai mult de jumătate din dimensiunea sa. 185. Exerciții. 1. Sunt date două segmente AB și CD. Găsiți AB / CD, presupunând că aceste segmente sunt comensurabile; apoi găsiți CD / AB (sau: măsurați segmentul AB, luând CD-ul ca unitate liniară și, invers, măsurați CD-ul, luând AB ca unitate). 2. Sunt date două segmente. Găsiți valoarea aproximativă a raportului lor, presupunând că cel de-al treilea rest, atunci când își găsesc măsura comună, poate fi considerată ca măsură comună. Se dau două segmente (incomensurabile). Găsiți raportul lor la 1/8; apoi găsiți cu aceeași precizie raportul lor invers (măsurați cu cel mai apropiat 1/8 primul segment, luați cel de-al doilea și, invers, măsurați cu aceeași precizie cel de-al doilea segment, luând primul).
La punctul 170 există înregistrări corespunzătoare despre relația AB / CD, și anume: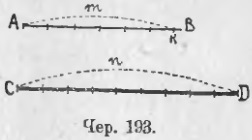
Articole similare