Băieți, am construit multe grafice de funcții, de exemplu, parabole, hiperbola, grafice de funcții trigonometrice și altele. Să ne amintim cum am făcut-o. Am ales punctele pe axa absciselor, am calculat ordonatele funcțiilor noastre și ne-am conectat linia ordonată pe planul de coordonate. Asta este, am complotat pe puncte. Când se construiesc mai multe grafice, punctele trebuie alese în mod deliberat. Acum, să ne rezumăm cunoștințele și să scriem regulile generale pentru plotarea funcțiilor.
Ce este un grafic de funcții?
Un grafic de funcții este un set de puncte ale căror abscise sunt valori din domeniul definiției, iar ordonatele sunt valorile funcției y = f (x). Graficul fiecărei funcții este construit de puncte. Dar dacă nu știm exact ce arăta harta, atunci punctele ar trebui alese în mod deliberat. Băieți, ce puncte importante are funcția?
Să le amintim:
a) Puncte staționare și critice. Am învățat astfel de puncte în calcularea extremelor funcțiilor. Acesta este punctul în care derivatul este fie zero, fie nu există.
b) Puncte extreme. Puncte de maximă și minimă de funcții. Puncte la care caracterul de monotonie este determinat.
c) punctele de intersecție a graficului cu abscisa și axa ordinii. Valorile în care funcția y = f (x) = 0 este punctul de intersecție cu abscisa. Și dacă vom calcula f (0), atunci acest punct de intersecție cu axa ordonată.
d) Puncte de discontinuitate a funcțiilor. Aceste puncte sunt căutate pentru funcții non-continue.
Regula pentru plotarea funcțiilor
Băieți, să scriem regulile de bază pentru plotarea funcțiilor:
- Dacă funcția y = f (x) este continuă pe linia reală întreg, trebuie să găsim puncte de staționare și critice, punctul extremelor, intervale de monotonie, punctul grafic de intersecție cu axele de coordonate și alege câteva puncte de control după cum este necesar, ceea ce ar trebui să calculeze valoarea funcției noastre .
- Dacă funcția y = f (x) nu este definită pe întreaga linie de număr, atunci ea începe cu găsirea domeniului definiției funcției, cu punctele de discontinuitate.
- Este util să se examineze funcția pe paritate, deoarece grafica chiar sau funcții impare au simetrie (în raport cu axa y, respectiv, sau în raport cu originea), și, prin urmare, este posibil să se construiască primă ramură a graficului numai dacă x ≥ 0, și apoi pentru a termina o ramură simetrică.
- Dacă acea linie y = b este o asimptote orizontală a graficului funcției noastre. Asymptote este un punct de referință pentru funcția noastră. Acesta este motivul pentru care graficul funcției în acest punct tinde, dar nu atinge această valoare.
- Dacă f (x) = $ \ frac $; iar pentru x = a numitorul dispare și numărul este nenul, atunci x = a este asimptota verticală.
Mai multe reguli care simplifică construirea grafurilor de funcții:
a) Graficul grafului funcției y = f (x) + a este obținut din graficul funcției y = f (x) (graficul y = f (x) este cunoscut în prealabil) prin transfer paralel al grafului y = f (x) a> 0; și aa în jos dacă a 2. b) y = x 2 + 2, c) y = x 2 - 3.
Graficele funcțiilor noastre sunt obținute din graficul funcției y = x 2. prin traducere paralelă: b) două unități în sus, c) trei unități în jos.
Grafice ale funcțiilor noastre:
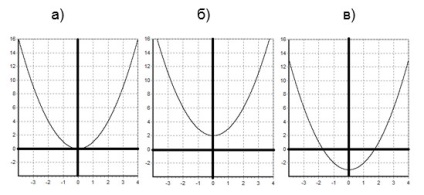
b) Graficul grafului funcției y = f (x + a) este obținut din graficul funcției y = f (x) (graficul y = f (x) este cunoscut în prealabil). Folosim transferul paralel al grafului y = f (x) cu o unitate la stânga dacă a> 0 și aa unități spre dreapta, dacă a 2. b) y = (x + 1) 2.
Graficele funcțiilor noastre sunt obținute din graficul funcției y = x 2. prin transferul său paralel: b) două unități spre dreapta, c) o unitate la stânga.
Grafice ale funcțiilor noastre:
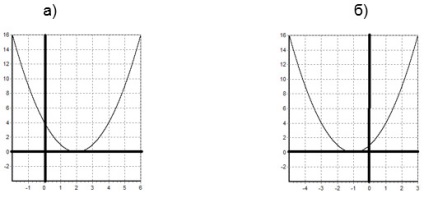
c) Pentru a compune graficul funcției y = f (-x), trebuie să plotăm graficul funcției y = f (x) și să o reflectăm în raport cu axa ordinii. Graficul rezultat este graficul funcției y = f (-x).
Pentru un exemplu, să construim două grafice: a) y = x 3. b) y = (-x) 3.
Graficele funcțiilor noastre sunt obținute din graficul funcției y = x 3. prin reflectarea de la axa y.
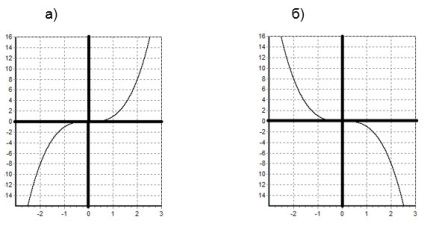
d) Pentru a plota graficul funcției y = -f (x), compuneți funcția y = f (x) și reflectați-o în raport cu abscisa.
Pentru un exemplu, construim două grafice: a) y = cos (x), b) y = -cos (x). Graficele funcțiilor noastre sunt obținute din graficul funcției y = cos (x), prin reflectarea față de abscisă.
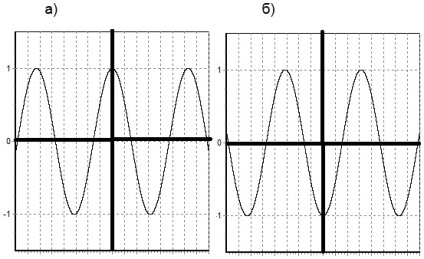
Băieți, acum să construim grafice de funcții, a căror formă nu este cunoscută în prealabil. Vom folosi regulile pe care le-am definit la început.
Exemple de construcție
I. Construiește un grafic funcțional: y = 2x 2 + 4x - 5.
soluţie:
1) Domeniul definiției: D (y) = (-∞; + ∞).
2) Să găsim punctele staționare:
y '= 4x + 4,
4x + 4 = 0,
x = -1.
3) Definim forma punctului staționar și caracterul monotonicității:
Punctul x = -1 este punctul minim. Să găsim valoarea funcției la punctul x = -1
y (-1) = 2 (-1) 2 + 4 (-1) -5 = -7.
Deci, funcția noastră scade pe intervalul = (- ∞; -1), x = -1 este punctul minim, funcția crește pe intervalul (-1; + ∞).
Calculam valorile funcției într-o pereche de puncte:
Să construim graficul funcției:
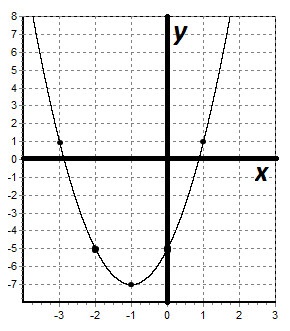
II. Construiește un grafic funcțional: y = 5x 3 - 3x 5.
soluţie:
1) Domeniul definiției: D (y) = (-∞; + ∞).
2) Să găsim punctele staționare:
y '= 15x2 - 15x4,
y '= 15x2 (1-x2) = 15x2 (1-x) (1 + x)
15x2 (1 - x) (1 + x) = 0,
x = 0; ± 1.
3) Definim forma punctului staționar și caracterul monotonicității:
Punctul x = -1 este punctul minim.
Punctul x = 0 este punctul de inflexiune, funcția în acest moment crește, de asemenea, dar concavitatea se schimbă în cealaltă parte.
Punctul x = 1 este punctul maxim.
Să găsim valoarea funcției la punctul x = -1: y (-1) = 5 (-1) 3 - 3 (-1) 5 = -2.
Gasim valoarea funcției în punctul x = 0: y (0) = 5 (0) 3 - 3 (0) 5 = 0.
Să găsim valoarea funcției la punctul x = 1: y (1) = 5 (1) 3 - 3 (1) 5 = 2
5) Să investigăm funcția prin paritate: y (-x) = 5 (-x3) -3 (-x5) = -5x3 + 3 5 = -y (x)
Prin definiție, funcția este ciudată, iar graficul este simetric în raport cu originea.
Deci, funcția este ciudată.
Funcția noastră scade pe un interval egal cu (-∞; -1).
x = -1 este punctul minim. Funcția crește cu (-1; 1).
x = 0 este punctul de inflexiune.
x = 1 este punctul maxim. Funcția crește cu (1; + ∞).
Calculam valorile funcției într-o pereche de puncte:
Să construim graficul funcției:
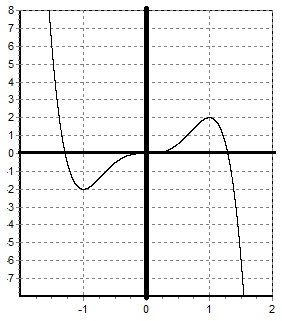
III. Construiește un grafic de funcții: y = $ \ frac $.
soluţie:
1) Domeniul definiției: D (y) = (-∞; -2) U (-2; 2) U (2; + ∞).
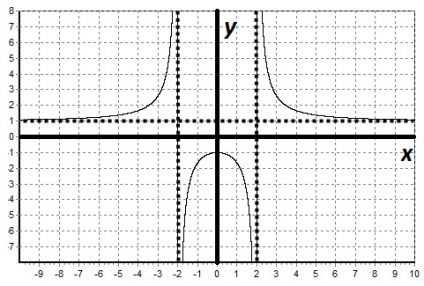
Prin definiție, funcția este uniformă. Prin urmare, funcția de schemă de tratament este simetrică în raport cu axa verticală se poate construi mai întâi un grafic al funcției pentru x ≥ 0. 3) x = 2 Direct - asimptotă verticală, deoarece numitorul funcției noastre dispare în acest moment.
Să găsim asimptotul orizontal:
Linia dreaptă y = 1 este asimptota orizontală.
4) Să găsim punctele staționare și critice:
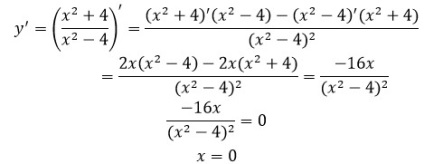
5) Definiți forma punctului staționar și caracterul monotonicității: Punctul x = 0 este punctul maxim.
Deci, funcția noastră este chiar. Se mărește în intervalul egal cu (-∞; 0), x = 0 este punctul maxim. Funcția scade cu (0; + ∞).
Linia dreaptă x = 2 este asimptota verticală. Linia dreaptă y = 1 este asimptota orizontală.
Calculam valorile funcției într-o pereche de puncte:
pentru că chiar și atunci când construim un grafic pentru x ≥ 0.
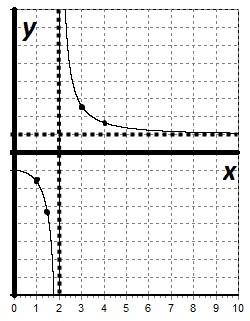
Folosind proprietatea funcțiilor uniforme, reflectăm graficul funcției în raport cu axa de coordonate.
Sarcini pentru plotarea funcțiilor pentru soluții independente
1) Construiește un grafic al funcției: $ y = (-x) ^ 2 + 4x - 7 $.
2) Construiește un grafic al funcției: $ y = x ^ 3 - 3x + 2 $.
3) Construiți un grafic de funcții: $ y = \ frac $.