Ecuația oscilației unui punct are următoarea formă: x = Asin (wt + pi (0)). Aici A este amplitudinea oscilațiilor, w este frecvența oscilațiilor și fi (0) este faza inițială a oscilațiilor. Din păcate, în BV, literele grecești nu pot fi folosite, așa că în loc de omega am scris w și în loc de scrisoarea greacă phi pe care am scris-o în limba rusă. Faza inițială a oscilațiilor este egală cu zero, adică ψ (0) = 0. Apoi ecuația oscilațiilor noastre va fi
În momentul inițial al timpului, pentru t = 0, avem Asin (wt) = 0, apoi x (0) = 0. Am uitat deja ce clasă trec derivatele. Pentru a găsi o ecuație pentru viteza v a oscilațiilor, trebuie să luăm derivarea timpului de ecuație (1). Avem
În momentul inițial al timpului (t = 0), cos (wt) = 1. Viteza de oscilație va fi maximă și egală cu v (max) = wA. O perioadă de oscilații = 2n, unde pi = 3.14 este litera greacă pi.
Perioada de oscilație este de obicei indicată prin litera T. Avem wT = 2n. Sau perioada T = 2n / w. În problema se spune, atunci când viteza unui punct devine egală cu jumătate din viteza maximă. Aceasta este, v = v (max) / 2 = wA / 2 = 0,5wA. Din ecuația 2 este necesar să găsim acest timp t. Avem
0,5wA = wAcos (wt). De aici găsim cos (wt) = 0,5. Cosinul este 0,5 (sau 1/2) atunci când wt = pi / 3. Aceasta este din trigonometrie. Găsiți t = pi / 3w. Dar w = 2n / T. Atunci avem
t = pi / 3w = piT / (3 * 2n) = T / 6, unde * este semnul de multiplicare. Răspuns: viteza punctului de oscilație va fi egală cu jumătate din viteza maximă la T / 6, adică 1/6 din perioada de oscilație.
Și acesta este un grafic al oscilațiilor armonice
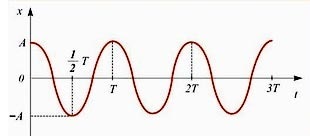
Iată un grafic al modificării vitezei cu timpul. Aici, pe verticală, trebuie să amânăm viteza v, nu x. Și amplitudinea este WA, nu A.