Funcții: \ (f \), \ (u \), \ (v \)
Argument (variabilă independentă): \ (x \)
Derivatul funcției: \ (y '\ stânga (x \ right) \), \ (f' \ stânga (x \ right) \)
Constanta: \ (C \)
Numerele reale sunt: \ (A \), \ (\ alpha \)
Creșterea funcției: \ (\ Delta y \)
Creșterea variabilei independente este: \ (\ Delta x \)
Diferența funcției: \ (dy \)
Diferența variabilei independente: \ (dx \)
Să considerăm funcția \ (y = f \ stânga (x \ dreapta) \) și presupunem că la un moment dat \ (x \) Argumentul este incrementată \ (dx \), care se numește un diferențial al variabilei independente. Funcția \ (y = f \ stânga (x \ dreapta) \) are o diferență de la punctul \ (x \), în cazul increment acesteia poate fi reprezentat ca suma a doi termeni:
\ (Delta y = f \ stânga (\ dreapta) - f \ stânga (x \ dreapta) = A \ Delta x + \ alpha, \)
unde coeficientul \ (A \) nu depinde de \ (\ Delta x \), iar valoarea \ (\ alpha \) are un ordin mai mare de micime în trepte \ (\ Delta x \), adică \ (\ alpha / \ Delta x \ to 0 \) pentru \ (\ Delta x \ to 0 \).
Formula înregistrată partea lineară principală a creșterii se numește funcția diferențială \ (f \ stânga (x \ dreapta) \) la punctul \ (x \), și este notat ca \ (dy = A \ Delta x \). În această expresie, coeficientul \ (A \) este valoarea derivatei \ (f „\ stânga (x \ dreapta) \) la punctul \ (x \).
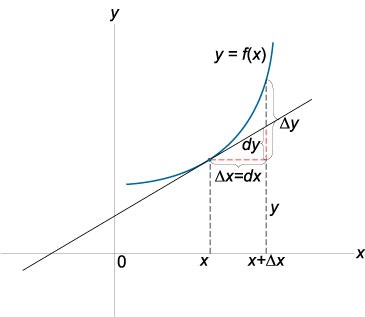
Diferența unei variabile independente este egală cu creșterea acesteia:
\ (dx = \ Delta x \)
Diferența funcției este egală cu produsul derivatului prin diferența dintre variabila independentă:
\ (dy = df \ stânga (x \ dreapta) = f '\ stânga (x \ dreapta) dx \)
Expresia derivatului în termeni de diferențieri
\ (f '\ stânga (x \ dreapta) = \ mare \ frac >> \ normalizați \)
Diferența unui număr constant este egală cu zero:
\ (dC = 0 \)
Diferența dintre suma funcțiilor este egală cu suma diferențelor:
\ (d \ stânga (\ dreapta) = du + dv \)
Diferența diferenței de funcții este egală cu diferența dintre diferențiale:
\ (d \ stânga (\ dreapta) = du-dv \)
Factorul constant poate fi luat ca semn al diferențialului:
\ (d \ left (\ right) = Cdu \)
Diferențial al produsului funcțiilor
\ (d \ stânga (\ dreapta) = vdu + udv \)