Prezentare pe tema: "DESIGNUL CENTRAL Împreună cu proiecțiile paralele și ortogonale folosite în geometrie pentru imaginea formelor spațiale, minunate". - Transcriere:
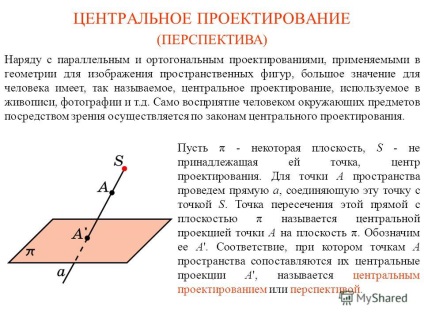
1 proiecția centrală Împreună cu proiecții paralele și ortogonale, utilizate în geometria cifrelor spațiale de imagine, de o mare importanță pentru om este așa-numita proeminență centrală utilizată în picturi, fotografii, etc. Percepția obiectelor înconjurătoare de către ochi se realizează în conformitate cu legile designului central. Să fie un plan, un punct non-punct, un centru de proiecție. Pentru punctul A al spațiului desenați o linie care leagă acest punct cu punctul S. Punctul de intersecție al acestei linii cu planul π este numit proiecția centrală a punctului A pe planul π. Noi o numim cu A '. Corespondența în care punctele A ale spațiului sunt asociate cu proiecțiile lor centrale A 'se numește proiecție centrală sau perspectivă. (OUTLOOK)
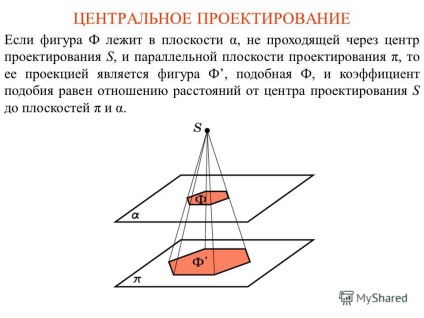
2 proiecție centrală Dacă figura F se află în planul a, nu trece prin centrul de design S, și paralel cu tt planul de proiecție, atunci proiecția sa este figura F, această F, iar raportul de similaritate este raportul dintre distanța de la centrul de proiecție S la planurile tt și α.
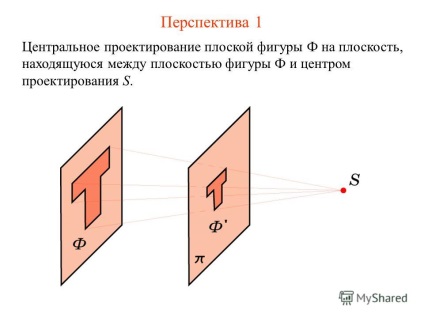
3 Perspectiva 1 Proiecția centrală a unei figuri plane Φ pe un plan situat între planul figurinei Φ și centrul de proiecție S.
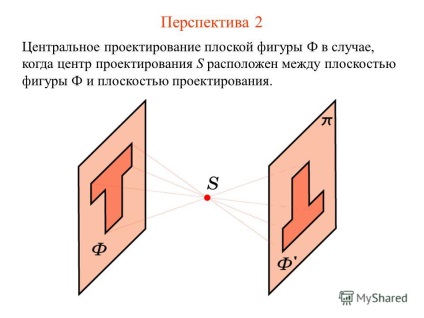
4 Perspectiva 2 Proiecția centrală a unei figuri plane F în cazul în care centrul de proiectare S este situat între planul figurinei Ф și planul de proiectare.
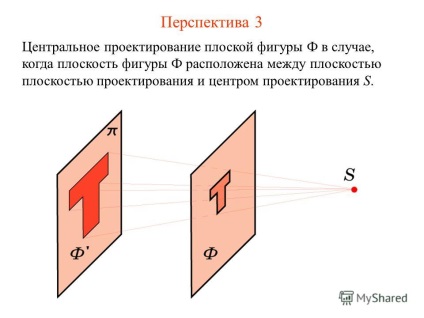
5 Perspectiva 3 Proiecția centrală a figurii plane Φ în cazul în care planul figurinei Φ este situat între planul planului de proiecție și centrul de proiecție S.
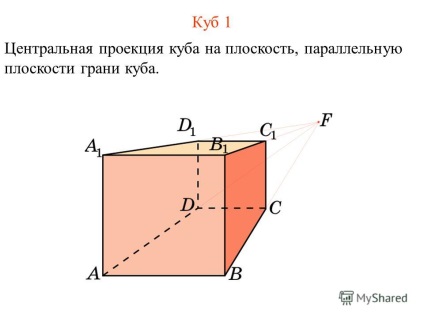
6 Cubul 1 Proiecția centrală a cubului pe un plan paralel cu planul feței cubului.
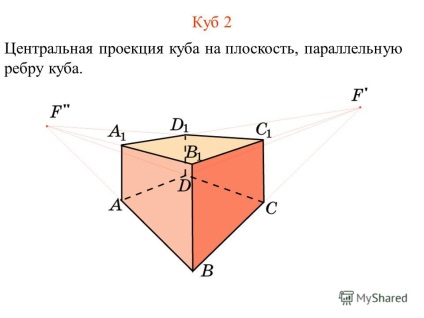
7 Cubul 2 Proiecția centrală a cubului pe un plan paralel cu marginea cubului.
8 Cubul 3 Proiecția centrală a cubului în cazul general.
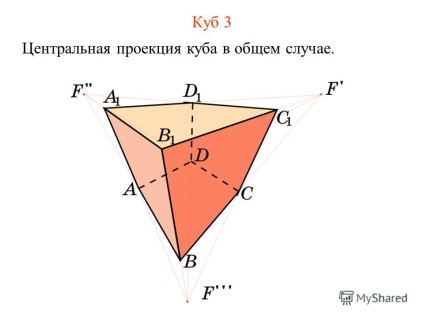
9 Cubul 4 Proiecția centrală a cubului în cazul general.

10 Piramida Proiecția centrală a piramidei cvadrangulare regulate.
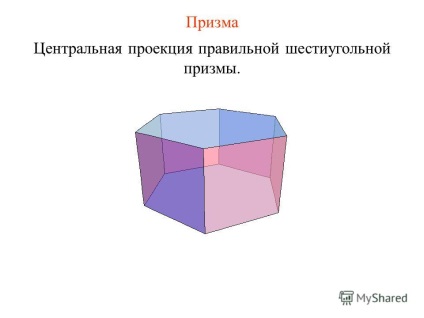
11 Prism Proiecția centrală a unei prisme hexagonale regulate.
12 Cilindrul Proiecția centrală a cilindrului.
13 A. Durer Gravura lui A. Durer (1471 - 1528) arată primirea unei imagini în perspectivă a unui obiect cu ajutorul unui fir întins.

14 N.N. Ge rus artist și profesor NN. Ge (1834-1894), adresându-se ucenicilor săi, a spus: "Învățați perspectiva și când o stăpâniți, aduceți-o în lucrare, în desen. Aici vom prezenta o imagine a lui N.N. Ge "Petru I interoghează pe Tsarevich Alexei"
15 I.E. Repin () Nu este de așteptat
17 Exercițiul 1 Există o proiecție centrală pentru toate punctele din spațiu? Pentru care puncte nu există? Răspuns: Nu. Nu există pentru punctele unui plan care trece prin centrul de proiectare și paralel cu planul de proiecție.
18 Exercițiul 2 Pot paralele paralele să treacă la intersecția în proiectarea centrală? Răspuns: Da.
19 Exercițiul 3 În ce caz va fi proiecția centrală a două linii să fie două linii paralele? Răspuns: Dacă liniile sunt paralele cu planul de proiecție.
20 Exercitarea 4 Care imagine a figurii va fi obținută în proiecția centrală, dacă planul de proiectare este situat între figură și centrul de proiectare? Răspuns: Reducerea directă.
21 Exercițiul 5 Care imagine a figurii va fi în proiecția centrală, dacă centrul de proiectare se află între figură și planul de proiectare? Răspuns: inversat.
22 Exercițiul 6 Care imagine a figurii va fi obținută în proiecția centrală, dacă aceasta se află între planul de proiectare și centrul de proiectare? Răspuns: Creșterea directă.
23 Exercitarea 7 Cum rămâne cu proiecția centrală a unei figuri plane situate într-un plan paralel cu planul de proiecție? Răspuns: Va fi similar cu cel original.
Exercițiul 8 Liniștea să se intersecteze cu avionul și să nu treacă prin punctul S. Arată în figura unde, în proiecția centrală, o parte a liniei drepte a este situată: a) "mai mare"; b) "sub" planul. Raspuns: a) La punctele din raze AD si SC fara inceputuri, adica fără punctele A și S; b) la punctele segmentului AS fără capete, adică fără punctele A și S.
25 Exercițiul 9 Figura prezintă proiecția centrală a cubului. Explicați modul în care, în fiecare caz, cubul este poziționat în raport cu planul de proiectare. Răspuns: a) Fața ADD 1 A 1 a cubului este paralelă cu planul de proiecție; b) marginea BB 1 a cubului este paralelă cu planul de proiecție; c) fața ABCD a cubului este paralelă cu planul de proiecție și punctul F se află în interiorul imaginii acestei fețe; d) planul de proiectare nu este paralel cu nici o margine a cubului.
26 Exercițiul 10 Figura prezintă proiecția centrală a piramidei patrulaterale corecte. Explicați modul în care este poziționată în raport cu planul de proiectare. Răspuns: a) Planul bazei piramidei este paralel cu planul de proiecție, iar linia dreaptă SM este perpendiculară pe planul de proiecție, unde S este centrul de proiectare, M este vârful piramidei; b) planul bazei piramidei este paralel cu planul de proiecție; c) planul bazei nu este paralel cu planul de proiecție.
27 Exercițiul 11 Figura prezintă proiecția centrală a unui cilindru circular drept. Cum se poziționează cilindrul față de planul de proiectare? Răspuns: Planul de proiectare este paralel cu baza buteliei.
28 Exercitarea 12 Desenați proiecția centrală a cubului ABCDA 1 B 1 C 1 D 1 pe un plan paralel cu planul feței ABB 1 A 1. Răspuns.
Exercitarea 29 13 Distanța de la centru spre planul de proiecție al feței 1 A 1 ABB cub ABCDA 1 B 1 C 1 D 1 prezentată în figură este 10. Găsiți distanța de la planul median al feței sus Design CDD C 1 1. Răspuns. 20.
30 Exercițiul 14 Desenați proiecția centrală a cubului ABCDA 1 B 1 C 1 D 1 pe un plan paralel cu planul feței ABB 1 A 1. Răspuns.
31 Exercițiul 15 Distanța de la centrul de proiectare până la planul frontal al cubului CDD 1 C 1 ABCDA 1 B 1 C 1 D 1 prezentat în figură este 16. Gasiti marginea cubului. Răspuns. 8.
32 Exercitarea 16 Desenați proiecția centrală a cubului ABCDA 1 B 1 C 1 D 1 pe un plan perpendicular pe marginea AA 1, centrul de proiecție S se află pe extensia acestei muchii. Răspuns.
33 Exercitarea 17 Desenați proiecția centrală a cubului ABCDA 1 B 1 C 1 D 1 pe un plan care nu este perpendicular pe marginea AA 1, centrul de proiecție S se află pe extensia acestei muchii. Răspuns.
Exercitiul 34 18 Desenați centrală de proiecție cub ABCDA 1 B 1 C 1 D 1 pe un plan perpendicular pe AC diagonal 1, centru de proiectare S se află pe extensia diagonalei. Răspuns. Cifrele arată imaginile obținute cu ajutorul programelor de calculator.
35 Exercițiul 19 Un singur cub ABCDA 1 B 1 C 1 D 1 este proiectat pe planul feței ABB 1 A 1. Latura pătratului care este proeminența feței CDD 1 C 1 este egală cu 0,4. Găsiți distanța de la centrul de proiectare până la planul de proiectare. Răspuns.
36 Exercițiul 20 Desenați o proiecție centrală a piramidei drepte patrulaterale SABCD pe un plan perpendicular pe marginea AS, centrul de proiecție S se află pe extensia acestei muchii. Răspuns.
Exercitiul 37 21 Desenați proiecția centrală a unei prisme hexagonale regulate ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 pe un plan perpendicular pe OO segmentul 1 care leagă centrul bazei sale, centrul de proiecție S se află pe continuarea acestui segment. Răspuns.
Exercitiul 38 22 regulate prisme hexagonale ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, marginile de care sunt 1, este proiectat pe planul feței A 1 B 1 C 1 D 1 E 1 F 1. Părțile laterale ale hexagonului, care se confruntă cu proiecție ABCDEF sunt egale cu 0,6. Găsiți distanța de la centrul de proiectare până la planul de proiectare. Răspuns. 1.5.
Exercitiul 39 23 Desenați proiecția centrală a unei prisme hexagonale regulate ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 pe un plan perpendicular pe muchia AA 1, centru de design S se află pe extinderea coastelor. Răspuns.
Exercitiul 40 24 Desenați proiecția centrală a unei prisme hexagonale regulate ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 pe un plan perpendicular pe segmentul care unește centrele fețelor laterale opuse, centru de design S se află pe continuarea acestui segment. Răspuns.
Exercitiul 41 25 Desenați proiecția centrală a unei prisme hexagonale regulate ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 pe un plan perpendicular pe segmentul care unește punctele de centru marginile laterale opuse, în spațiul central S designul se află pe continuarea acestui segment. Răspuns.