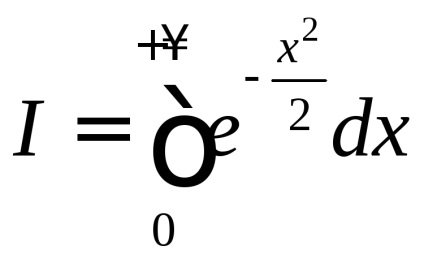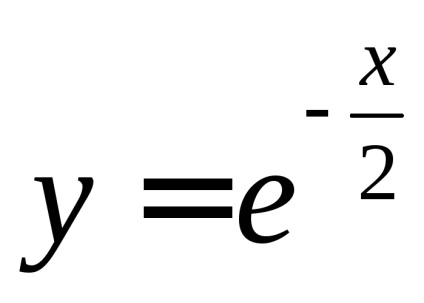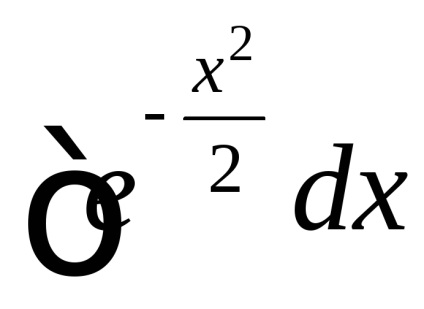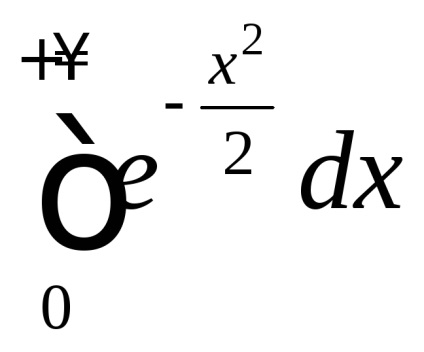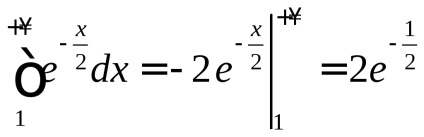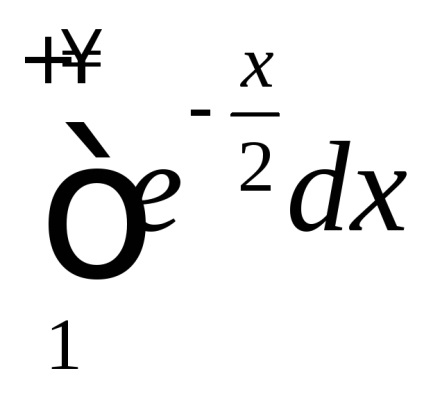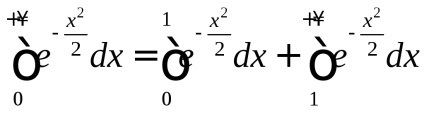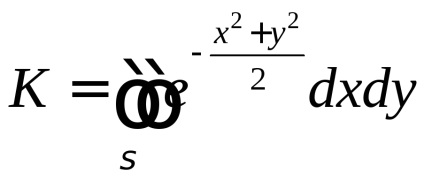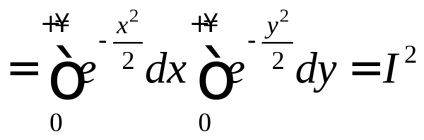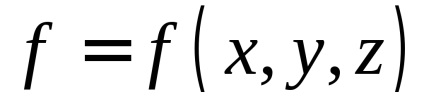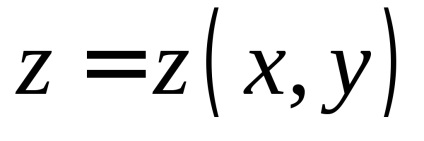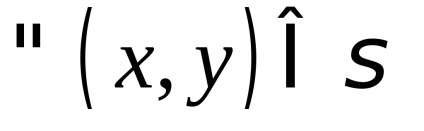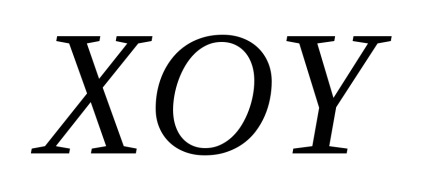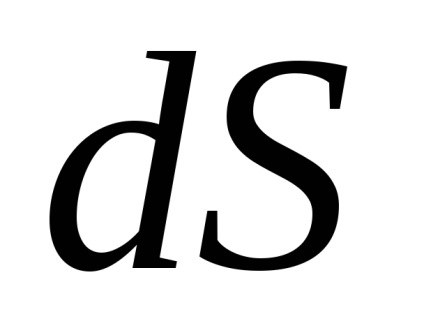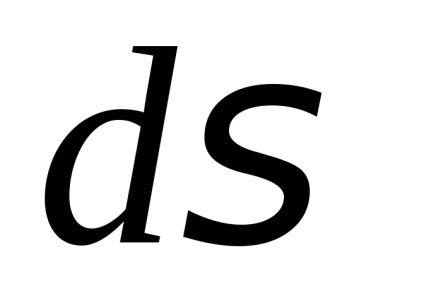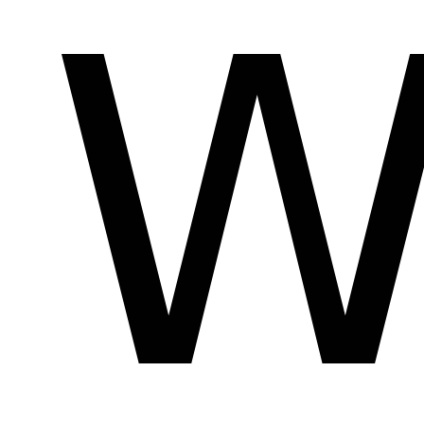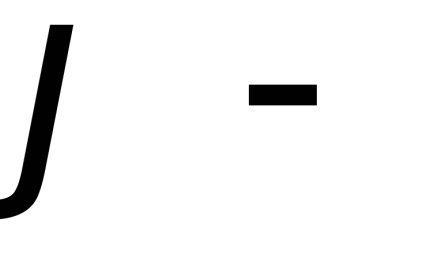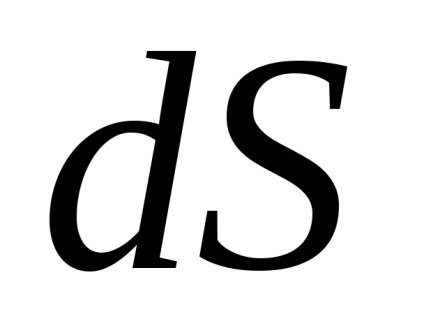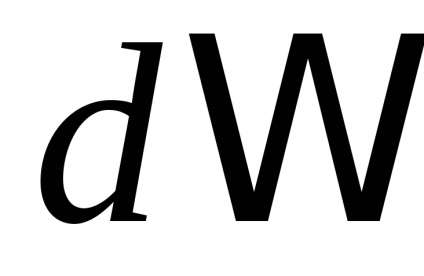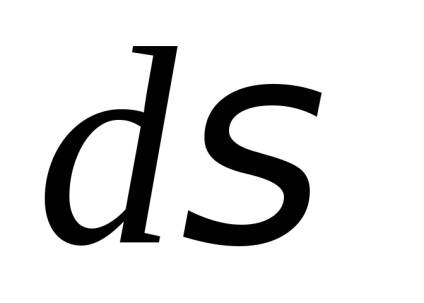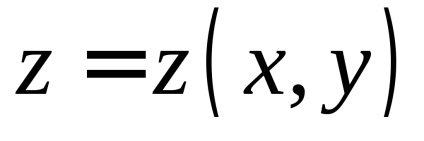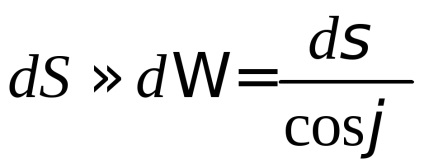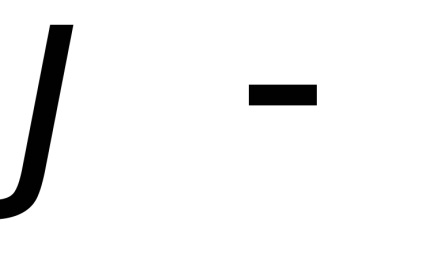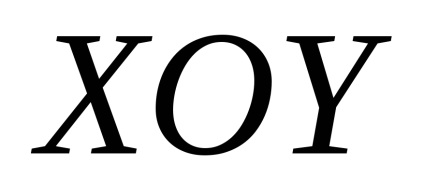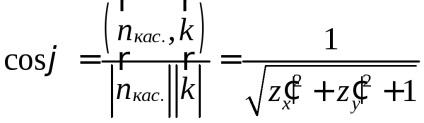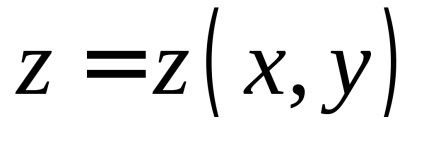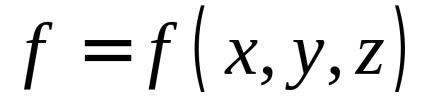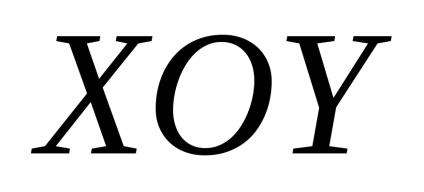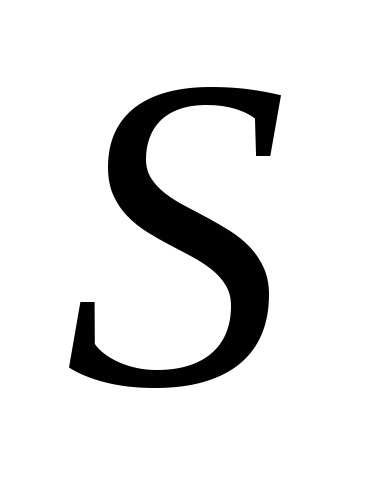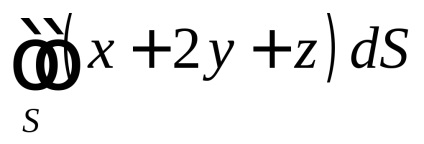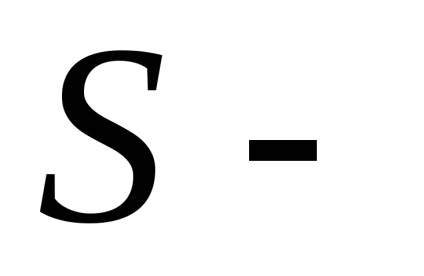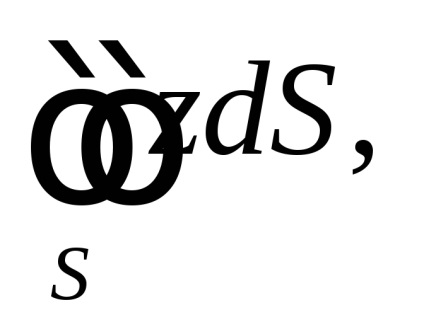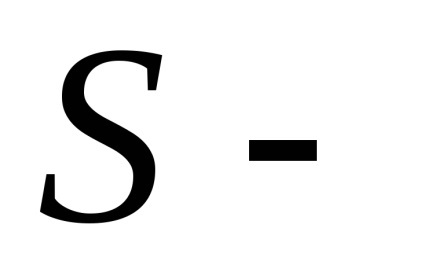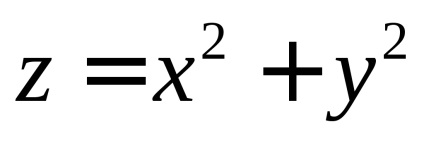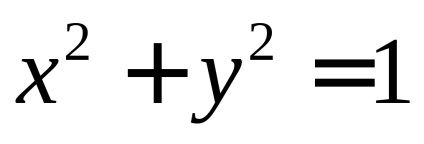În teoria probabilității un rol important îl joacă un integral necorespunzător
, care este numit integral Poisson. După cum este menționat în capitolul 7, funcțianu are un element antiderivativ elementar și integralul nedefinitse referă la așa-numitele integrale "neconverse". Cu toate acestea, pentru a calcula necorespunzătoarepoți. Înainte de a-și găsi sensul, vom vedea că aceasta converge.De atunci, dar
, adică prin definirea convergenței integralelor necorespunzătoare ale genului converge. prin urmareconverge pe baza comparației.
Pentru a calcula valoarea integratului Poisson, aplicăm această metodă artificială: considerăm integralele duble
, unde aria de integrare este primul trimestru al planului de coordonate (figura 56).
În coordonate carteziene
(ne amintim că valoarea unui integral integrat nu depinde de desemnarea variabilei de integrare).
Pe de altă parte, trecând la sistemul de coordonate polare, primim:
.
8.13. Calcularea integrala de suprafata a primului tip (suprafata)
Să presupunem că la suprafață
, definită de ecuație, o funcție continuă. Prin definiție, se numește un element de suprafață al primului tip al acestei funcții
,
în cazul în care punctele, și
- părți mici ale suprafeței, la care este rupt atunci când se compilează suma integrală (figura 10).
Presupunem că funcția
diferențiabilă, adică, în orice punct S se poate desena un plan tangent.
regiune
este o proiecțieîn avion. Exprimăm elementul de suprafațăprin proiecția sa(Figura 57). Pentru aceasta folosim afirmația binecunoscută că dacă - proiecția unei zone plate cu o suprafață de, , undeUnghi între planul regiunii și planul de proiecție.
Desenăm într-un punct arbitrar elementul selectat al suprafeței
tangent avion și să lăsați- partea pe care se proiectează. Deoarece funcțiaeste diferențiată, apoi suprafața elementului, undeunghiul dintre planul tangent și plan, care este egal cu unghiul dintre normalele lor.
Noi calculam
. Dacă rescriim ecuația de suprafațăîntr-o formă implicită, atunci (vezi capitolul 6), atunci,(vezi capitolul 2).
În punctele de pe suprafață
, unde, funcție ia valori, prin urmare, în conformitate cu definiția, integrale de suprafață a primului tip poate fi redusă la un integrat dublu:
Astfel, calculul integrității de suprafață a primului tip reduce la calcularea integrala dublă de la proiecția suprafeței date pe plan
.
NOTĂ. Dacă suprafața
este convenabil să se proiecteze pe un alt plan de coordonate, apoi formulele (8.17) și (8.18) se vor schimba în consecință.
P
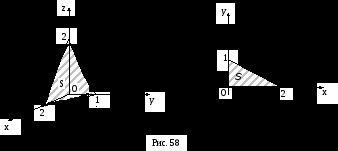
Versificator. calcula , dacăo parte din planul situat în primul octant (figura 58).
Din ecuația avionului obținem:
. În plus, în toate punctele planului, prin urmare, prin proprietatea 1 a integralului definit: zona proiecției
(Figura 58) este în mod evident egal cu 1.
Luați în considerare un exemplu puțin mai complex.
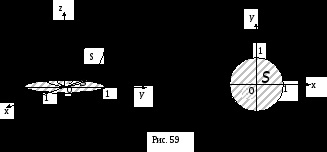
EXEMPLU. calcula
dacăo parte din suprafața unui paraboloid eliptic, sculptat din el de un cilindru(Figura 59).
Articole similare