Prismele sunt realizate din sticlă optică și folosite pentru a deflecta razele luminoase. Luați în considerare calea razelor de lumină din prisma triedească. Dacă o rază de lumină cade pe fața AB și părăsește chipul BC, fața BC este numită baza prismei, vezi Fig. Unghiul opus γ este numit unghiul refractar al prismei. Unghiul Δ între direcția razei 1 și direcția fasciculului deflectat 2 se numește unghiul de deformare a fasciculului în prisma. Unghiul la care prisma deviază (o rază monocromatică) a luminii depinde de unghiul de refracție al prismei γ, de indicele de refracție al prismei n și de unghiul de incidență α 1 (vezi figura)
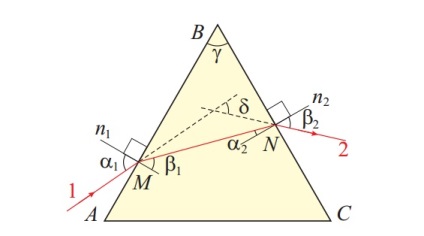
Fig. Raza 1 cade pe fața AB a prismei triere, este refractată, cade pe fața BC. refractează și frunze (grinda 2) din prisma. Când trece prin prisma, fasciculul de lumină este deflectat de un unghi Δ. care depinde de densitatea optică a materialului prismei n și de unghiul de refracție al prismei. Valorile normale n1 și n2 sunt arătate fețelor refracționale ale prismei. Se poate vedea că o rază de lumină care a trecut prin prisma este deviată la baza AC. Atunci când sunt refractate în punctul M, unghiurile de incidență α1 și refracția β1 sunt legate de egalitate
Din triunghiul MNB găsim unghiul de incidență α 2 al razei pe fața prismei BC. Unghiul completează unghiul β1 la un unghi drept, deci
În mod similar, unghiul completează unghiul α 2 la un unghi drept, deci
Deoarece suma unghiurilor din triunghi este Π. avem
Unghiurile α 2 și β 2 sunt legate de relația
La punctul M, fasciculul este deviat cu un unghi α 1 și β 1. și la punctul N - prin unghiul β 2 - α 2. Prin urmare, unghiul total de deformare a fasciculului Δ de prisma este egal cu suma abaterilor la punctele M și N
Substituind aici valoarea a 2 din (2), obținem
Utilizarea egalităților (1) - (4) și cunoașterea n și γ. este posibil să se calculeze unghiul Δ de deformare a fasciculului de către o prisă pentru fiecare unghi de incidență α 1.