În fereastra rezultatelor finale, va fi emis un tabel, care este prezentat mai jos. Aceasta va reflecta indicatorii principali și intermediari ai criteriului Kolmogorov-Smirnov. Indicatorul principal, adică valoarea reală a criteriului este localizată în tabelul de pe linia "Cele mai extreme diferențe absolute" (discrepanța maximă absolută dintre curba experimentală și curba normală de distribuție). În acest exemplu, a fost D = 0,175.
Testul Kolmogorov-Smirnov dintr-un singur exemplu
a. Distribuția testului este Normală. b. Calculat din date.
Pentru interpretarea corectă a valorii criteriului obținut. Este necesar să se compare această valoare cu valoarea critică stabilită pentru acest criteriu. Valoarea critică este luată dintr-un tabel special, care poate fi găsit în manualele de statistică.
Pe scurt, putem spune că pentru a selecta valoarea critică dorită este necesar să se ia o linie care să corespundă numărului de persoane din proba experimentală minus 1 (această valoare este egală cu gradul de libertate a eșantionării). Apoi, în secțiunea "Verificarea unei singure probe", găsiți coloana în care este scris D0,05. apoi luați valoarea la intersecția cu rândul selectat - aceasta este valoarea critică a criteriului cu care trebuie să comparați valoarea obținută în SPSS.
De exemplu, numărul de membri din eșantionul dvs. (N) a fost de 36, așa cum este indicat în tabelul de mai sus. Prin urmare, gradul de libertate al eșantionului este: 36-1 = 35, atunci șirul trebuie selectat care indică numărul 35. Apoi, uite, ceea ce corespunde valorii critice a criteriului de D0,05. a fost egal cu 0,230. Prin compararea valorii experimentale a criteriului (0.175) cu valoarea critică (0,230), vedem că aceasta nu depășește acesta din urmă, din care concluzia privind absența unor diferențe semnificative între datele experimentale și distribuția distribuției normale. În cazul în care valoarea experimentală a fost egal cu sau mai mare decât valoarea critică, atunci concluzia ar fi fost diferit: de distribuție existente, a fost semnificativ diferită de distribuția normală.
Există un alt mod foarte popular de a evalua fiabilitatea diferențelor dintre distribuții sau anumite grupuri de date - se referă la un astfel de indicator ca la "nivelul de semnificație". Acest indicator este un indicator extrem de important pentru toate metodele statistice, astfel încât abilitatea de a le interpreta oferă o cheie pentru înțelegerea esenței rezultatelor prelucrării datelor statistice!
Dacă explicați esența indicatorului „nivelul de semnificație“, pe scurt, putem spune că arată măsura în care puteți avea încredere concluzia că există diferențe semnificative, cu alte cuvinte, cum greșit se poate dovedi această concluzie. În cazul în care inexactitatea ieșire este de numai 5%, ceea ce înseamnă că doar 5% din date nu susțin ipoteza unei diferențe semnificative, în timp ce restul de 95% din datele favorizează prezența unor diferențe semnificative între distribuțiile sau grupuri de date. În această situație, este în întregime posibilă acceptarea ipotezei diferențelor și recunoașterea acesteia ca fiind fiabilă, adică de încredere.
Nivelul de semnificație (de încredere), ipoteza este de obicei notat în cărțile de statistică prin litera „p“ (o abreviere a cuvântului „Probabilitatea“ - erori „probabil“ în producția, adică, reciproca a gradului de fiabilitate a producției).
Dar, pachete de nivel de semnificație statistică sunt, de obicei notate cu trei litere „sig este“ (o abreviere a cuvântului „semnificație“ - „relevanța“, adică „greutate“, valabilitatea retragerii). Valoarea nivelului de semnificație nu este de obicei exprimat în procente, și într-o fracțiune din întreg (câte unul): de exemplu, cinci la sută la nivel de ieșire inexactitate va fi denumit sig = 0,05, ceea ce corespunde la p = 0,05.
Chiar mai bine când nivelul este egal cu un sig inexactitate = 0,01, ceea ce indică faptul că 1% din datele nu sunt în concordanță cu ipoteza că prezența unor diferențe semnificative, datele de 99% confirmă această ipoteză, prin urmare, producția de diferențele vor fi foarte corecte sau de incredere se spune că este extrem de important.
În cazul în care indicatorul nivelului de semnificație SPSS (Sig) este p> 0,05, atunci nu se poate concluziona că există diferențe semnificative între distribuțiile comparate sau grupurile de date.
Regula decisivă în construirea concluziei privind fiabilitatea diferențelor poate fi exprimată după cum urmează:
In exemplul de mai sus, valoarea Sig, indicată în linia de jos a mesei, a fost la nivelul de 0,22, care depășește valoarea de 0,05 (p> 0,05), astfel încât este necesar să se tragă o concluzie cu privire la absența unor diferențe semnificative între obținute experimental și distribuția normală distribuirea de date. Cu alte cuvinte, distribuția obținută este suficient de apropiată de distribuția normală.
După cum puteți vedea, concluzia făcută de indicatorul nivelului de semnificație coincide cu concluzia făcută pe baza comparării valorilor criteriului însuși (calculat în SPSS și valoarea critică din tabel).
Pentru a verifica corectitudinea concluziilor, este posibil să se construiască distribuția frecvenței datelor experimentale care sunt disponibile în baza de date. Pentru aceasta, reveniți la tabela de baze de date (prin fila SPSS din bara de activități) și selectați comanda "Graphs". Apoi, selectați linia "Chart Builder", apoi se va deschide o fereastră în care trebuie să setați caracteristicile pentru plotarea graficului.
Alegerea caracteristicilor pentru plotarea distribuției frecvenței datelor
În rubrica "Alegeți din", trebuie să selectați o linie cu cuvântul "Histogramă". După aceasta, vor apărea mici imagini (modele) de construcție histogramă. Ar trebui să selectați, de exemplu, primul desen și să îl apăsați de două ori. Când se construiește o distribuție simplă a frecvenței pe câmpul din dreapta în fereastra "Statistică", se selectează "Frecvență Procent". După ce cursorul selectează această linie, butonul "Apply" din partea de jos a acestui câmp este apăsat în mod necesar, ceea ce duce la apariția acestei caracteristici pe axa de ordonare în fereastra grafică condiționată. Doar acum puteți să faceți clic pe butonul "OK" pentru a construi graficul.
Se deschide fereastra "Ieșire" cu graficul planificat (dacă nu, atunci apelați-o prin fila SPSS din bara de activități).
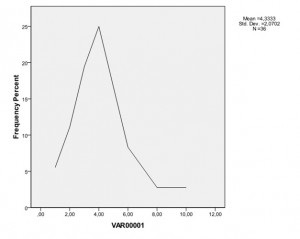
Curba distribuției frecvenței datelor (frecvența apariției rezultatelor este exprimată pur și simplu ca procent)
Din grafic se poate observa că cele mai frecvente (la nivelul de 25-20%) sunt valorile medii corespunzătoare valorilor rezultatelor în intervalul de la 3 la 6 unități. Și valori extreme, cum ar fi 1-2 sau 7-10, apar cu o frecvență de 7-5%. În consecință, în această distribuție, frecvența apariției valorilor medii domină în mod clar frecvența apariției unor valori extreme (scăzute și ridicate). Aceasta indică faptul că această distribuție are un caracter apropiat de cel normal, care este prezentat în figură.
Curba distribuirii normale a frecvenței apariției datelor (rezultatele testului) în eșantionul de subiecți
Astfel, numărul a demonstrat în mod clar concluzia că distribuția obținută în experiment nu are diferențe semnificative față de distribuția normală, ci, dimpotrivă, este destul de aproape de ea în natură. Distribuția, alta decât cea normală, are un caracter diferit.
Curba distribuirii frecvente a datelor non-normale
Distribuția datelor, în cazul în care rezultatele extreme sunt cu mult mai mari decât valorile medii, va fi semnificativ diferită de distribuția normală, după cum se arată în figură.
Dacă există o "înclinare" în intervalul de mijloc și există două "vârfuri" la margini, atunci o astfel de configurație a curbei poate însemna că eșantionul nu este omogen în compoziția sa, adică acesta combină două subgrupe de oameni, care diferă semnificativ unul față de celălalt în caracteristica studiată, ceea ce conduce la apariția a două vârfuri în distribuția de date.