Parchet geometric
Parchetul (sau mozaicul) este o familie infinită de poligoane care acoperă planul fără lumeni și acoperiri duble. Uneori, un parchet este o acoperire a unui avion cu poligoane regulate, în care două poligoane au o latură comună sau un vârf comun sau nu au deloc puncte comune; dar vom lua în considerare atât poligoane regulate, cât și neregulate. Deci, ce poligoane poate fi un plan de aplatizare?
Parchetele acelorași poligoane regulate
Suma tuturor unghiurilor n-gonului este de 180 ° (n-2). Toate unghiurile unui poligon obișnuit sunt egale; prin urmare, fiecare dintre ele este de 180 ° (n-2) / n. Fiecare vârf al parchetului converge un număr întreg de unghiuri; prin urmare, numărul 2 · 180 ° trebuie să fie un număr întreg de 180 ° (n-2) / n. Transformăm raportul dintre aceste numere:
Diferența n-2 poate lua doar valorile 1, 2 sau 4; prin urmare, n poate fi egal cu numai 3, 4 sau 6. Prin urmare, este posibil să se obțină parchete compuse din triunghiuri regulate, pătrate sau hexagoane regulate.
Parchete de la poligoane regulate diferite
În primul rând, să aflăm câte poligoane regulate (cu aceleași lungimi de laturi) pot fi în jurul fiecărui punct. Unghiul poligonului obișnuit trebuie să se situeze în intervalul de la 60 ° la 180 ° (nu include); prin urmare, numărul de poligoane din vecinătatea punctului trebuie să fie mai mare de 2 (360 ° / 180 °) și nu poate depăși 6 (360 ° / 60 °).
Se poate demonstra că există următoarele moduri de a așeza parchetul prin combinații de poligoane regulate: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) - două variante de parchet; (3,4,4,6) - patru opțiuni; (3,3,3,4,4) - patru opțiuni; (3,3,3,3,6); (3,3,3,3,3,3) (cifrele din paranteze - desemnează poligoane reuniți la fiecare nod 3 - un triunghi echilateral, 4 - pătrat, 6 - hexagon regulat, 12 - dodecagonal dreapta). Unele variante ale parchetului sunt prezentate în următoarele ilustrații:
Parchetele de poligoane neregulate
Este ușor să acoperiți planul cu paralelograme:
În general, este posibilă deschiderea planului cu copii ale unui patrulater arbitrar, nu neapărat convex:


Puteți face un parchet din copii ale unui triunghi arbitrar: de la două triunghiuri egale puteți adăuga un paralelogram și acoperiți planul cu copii ale paralelogramului.
Un alt plan poate fi acoperit cu copii ale unui hexagon simetric central sau copii ale unui pentagon cu două laturi paralele. Până în prezent, nu s-au găsit toate tipurile de pentagone convexe, din care se adaugă parchet. Dar demonstrarea teoremei este dovedită: "Este imposibil să dați un parchet din copii ale unui heptagon convex". În același timp, există parchete de heptagoni neconvexe:
Parchete de forme arbitrare
Unele definiții ale parchetului nu se limitează la poligoane; în acest caz, un parchet este o acoperire a unui plan fără omisiuni și suprapuneri prin figuri date (în cazul particular, poligoane, obișnuite sau neregulate, convexe sau neconvexe). În acest caz, chiar și pentru parchetele de poligoane, cerința "doi poligoane ar trebui să aibă un vârf comun, o parte comună sau nu au puncte comune" nu pot fi respectate; în plus, există multe parchete diferite, care nu constau în poligoane, ci cifre curbiliniere. Luați în considerare modalitățile de a construi un parchet nou, pe baza acestei definiții "extinse". Deci, cum să desenezi un parchet? (unele dintre căile posibile)
Metoda unu. Ia-o grilă (parchet deja cunoscute) - din triunghiuri echilaterale, hexagoane, pătrate sau poligon arbitrar, și efectuează conversia: compresie / expansiune, înlocuirea segmentelor de linie cu curbe de pornire și se termină la același punct ca și cea a segmentelor.
Exemplu: parchetele obținute prin înlocuirea segmentelor unei grile "pătrate" cu unele curbe sau linii întrerupte.
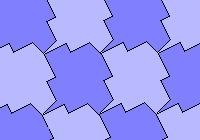
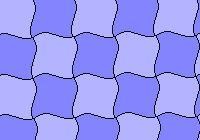

Metoda a doua. Am combinat elementele individuale ale parchetului existent. Exemple: parchet, obținut ca urmare a combinării elementelor unei rețele pătrate:



Parchet, fiecare element al căruia se obține prin combinarea a cinci triunghiuri regulate:

Calea a treia. Luăm grila existentă și o finalizăm cu noi linii. Avem o împărțire a avionului în figuri, care apoi pot fi reunite într-un mod nou. În cazul special, suprapunem două (sau mai multe) grile de parchete deja cunoscute, deplasându-ne sau rotuind o rețea față de cealaltă; Cifrele formate la intersecția liniilor sunt considerate elemente de parchet.
Exemplu (grilă se desparte de crucile grecești):
A patra metodă. Alegem o anumită curbă sau polilinie și începem să o transferăm la un vector, să ne rotim, să reflectăm. Curbele rezultate sau liniile sparte sunt plasate pe plan în așa fel încât să formeze contururi închise (care ulterior vor fi tratate ca elemente de parchet). Dacă luăm în considerare numai curbele neînchise și liniile sparte, parchetele se vor asemăna cu cele obținute prin metoda nr.1.
Pentru a obține următorul parchet, sa luat arcul spiralului, a fost rotit de trei ori cu 90 ° și apoi a fost aplicat un transfer paralel la figura rezultată.
Dar parchetele, obținute cu ajutorul transferului paralel al poligoanelor în formă de stea:


Combinând vârfurile de poligoane în formă de stea, obținem parchete constând din octogoane regulate, triunghiuri isosceles dreptunghiulare și, de asemenea, 16-gonde neconvexe care seamănă cu o cruce. În prima imagine există încă un element - un patrulater convex.
De asemenea, la pregătirea paginii, am folosit materialele pregătite de mine pentru UMK "Parchet geometric" ("Cum să desenez un parchet sau de ce nu există nici un fel de notebook într-un cerc").
Vezi și: Unsprezece parchete regulate pe site-ul Watermelon