PROBLEMA QUANTUM. Împământarea plăcii de condensatoare.
F65. Plăcile unui condensator plat sunt încărcate la potențiale + φ și -φ față de sol. Capacitatea condensatorului format de plăci. Equal C. și capacitatea condensatoarelor, care formează fiecare dintre plăci cu sol, C1. De câte ori se va modifica intensitatea câmpului electric între plăci, dacă unul dintre ele este legat la pământ.
Soluția.
Desenați un circuit de circuit echivalent.
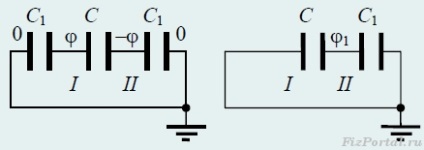
PROBLEMA QUANTUM. Acuzația unei mingi împământare.
F6. Găsiți ce încărcare a unei bile metalice împământate cu raza r este egală cu. dacă la o distanță R din centrul său există o sarcină q.
Soluția.
Potențialul mingii trebuie să fie zero. Potențialul câmp în centrul sferei, egal cu, desigur, potențialul mingea este format din potențialul domeniu al unei taxe q punct și câmpul creat de Q responsabil cu mingea. Încărcarea Q nu este uniform distribuită în jurul mingii. Dacă mingea este împărțită în zone mici cu taxe δq. potențialul câmpului produs de taxa minge în centru, poate fi exprimată ca un domeniu total de potențial al dq încărcare punct. Astfel, putem scrie pentru centrul mingii:
82 (165). Două bile mici de conducere cu raza r sunt situate la o distanță R una de cealaltă. Bilele sunt alternativ împământate pentru o vreme. Determinați potențialul mingii care a fost fundamentată mai întâi, dacă inițial fiecare minge avea o sarcină q.
Soluția.
Potențialul fiecărei mingi în funcție de principiul suprapunerii este egal cu suma potențialelor câmpurilor create prin sarcina proprie și încărcarea celeilalte minge.
După împământarea primei mingi, potențialul său este zero, adică
q1 / r + q / R = 0.
de unde
q1 = -qr / R.
În mod similar, pentru cea de-a doua minge după împământare, avem