Reprezentarea artistică a mașinii Turing
Turing Machine (MT) - executor abstract (computer abstract). A fost propusă de Alan Turing în 1936 pentru a formaliza conceptul de algoritm.
Mașina Turing este o extensie a automatului finit și, conform tezei Bisericii-Turing. este capabil să imite toți artiștii interpreți (prin specificarea regulilor de tranziție), realizând oarecum procesul de calcul pas cu pas, în care fiecare etapă a calculului este destul de elementară.
Adică, orice algoritm intuitiv poate fi realizat cu ajutorul unei mașini Turing [1].
Dispozitivul mașinii Turing [editați] edita wiki-text]
Mașina Turing include o bandă nelimitată în ambele direcții (mașinile Turing sunt posibile care au mai multe benzi infinite), împărțite în celule [2] [3]. și un dispozitiv de comandă (numit și un cap de citire / scriere) capabil să se afle într-o pluralitate de stări. Numărul de stări posibile ale dispozitivului de comandă este definit fin și precis.
Unitatea de control funcționează în conformitate cu regulile de tranziție. care reprezintă algoritmul implementat de această mașină Turing. Fiecare regulă de tranziție necesită aparatul, în funcție de starea actuală și observată în celula actuală de caractere, pentru a scrie în celulă un nou simbol, trece la o nouă stare și pentru a muta o celulă la stânga sau la dreapta. Unele stări ale mașinii Turing pot fi etichetate ca terminale. iar trecerea la oricare dintre ele inseamna sfarsitul muncii, oprirea algoritmului.
O mașină Turing se numește deterministă. dacă fiecare combinație de simbol de stare și bandă din tabel corespunde nu mai mult de o regulă. Dacă există o pereche de "simbol bandă - stare" pentru care există 2 sau mai multe comenzi, o astfel de mașină Turing este numită nondeterministică.
Descrierea mașinii Turing [edita] edita wiki-text]
Mașină specifică Turing este setat listarea set de elemente alfabet A, Q set de stări și un set de reguli prin care operează aparatul. Ei au forma :. Qi aj → qi1 AJ1 dk (în cazul în care capul este în qi de stat si a observat celule scrisoare scrisă aj cap se mută în statul qi1 celula în loc să aj înregistrat capul AJ1 face dk mișcare, care are trei opțiuni ....: celula la stânga (L), o celulă la dreapta (R), să rămână în (N)). Pentru fiecare configurație posibilă
Un exemplu de mașină Turing [edita] edita wiki-text]
Iată un exemplu de MT pentru înmulțirea numerelor într-un sistem de numere unare. reguli de înregistrare «qi aj → qi1 AJ1 R / L / N» ar trebui să fie înțeles după cum urmează: qi - o stare în care această regulă este îndeplinită, aj - datele din celula, care este cap, qi1 - starea în care aveți nevoie pentru a merge, AJ1 - aveți nevoie scrieți în celula, R / L / N - comanda de mutare.
Mașina funcționează în conformitate cu următorul set de reguli:
starea terminalului (oprirea algoritmului)
Înmulțiți cu MT 3 pe 2 în sistemul unității. Protocolul specifică starea inițială și cea finală a MT, configurația inițială pe bandă și locația capului mașinii (simbolul subliniat).
Începutul. Suntem în stare q0. introduceți datele mașinii: * 111x11 = *, capul aparatului se află pe primul simbol *.
Primul pas. Ne uităm la masa de reguli pe care mașina o va face, fiind în stare q0 și deasupra simbolului "*". Această regulă din prima coloană a rândului 5 este q0 * → q0 * R. Acest lucru înseamnă că ne îndreptăm într-o stare de Q0 (adică, nu se schimba), simbolul va fi „*“ (adică, nici o schimbare), și este părtinitoare «* 111x11 = *» la dreapta cu o poziție (R), am intrat text, și anume la primul caracter 1. La rândul său, starea q0 1 (prima coloană prima linie) este procesată de regula q0 1 → q0 1R. Asta este, încă o dată, du-te la dreapta cu o poziție. Acest lucru se întâmplă până devine simbolul "x". Și așa mai departe: să ia de stat (la indicele q), să ia caracterul la stand (caractere subliniate), și să le conectați pentru a viziona pentru procesarea tabelul de regulă combinația rezultată.
În cuvinte simple, algoritmul de multiplicare este: vom marca factorul prima unitate 2, înlocuind-o cu litera „a“, și trageți întregul factor 1 pentru un semn egal. Transferul se face prin înlocuirea alternativ unități primul multiplicator „un“ și alăturarea același număr de unități la sfârșitul liniei (din partea stângă a dreapta- „*“). Apoi vom schimba toate "a" la semnul de înmulțire "x" înapoi la unul. Și ciclul se repetă. Într-adevăr, un A multiplicat cu B poate fi reprezentat ca A + A + A B ori. Acum marcăm a doua unitate a celui de-al doilea factor cu litera "a" și transferăm din nou unitățile. Când nu există unități înainte de semnul "=", multiplicarea este finalizată.
Completitudine pentru Turing [edita] edita wiki-text]
Putem spune că mașina Turing este un calculator simplu cu memorie liniară, care, conform regulilor formale, convertește datele de intrare folosind o secvență de acțiuni elementare.
Acțiunea elementară este că acțiunea schimbă doar o mică bucată de date în memorie (în cazul mașinii Turing - o singură celulă), iar numărul de acțiuni posibile este finit. În ciuda simplității mașinii Turing, ea poate calcula tot ce poate fi calculat pe orice altă mașină care efectuează calcule folosind o secvență de operații elementare. Această proprietate se numește exhaustivitate.
Una dintre modalitățile naturale de a demonstra că algoritmii de calcul care pot fi implementați pe o singură mașină pot fi implementați pe de altă parte, este simularea primei mașini pe cea de-a doua.
Așa cum sa spus, pe mașina Turing este posibil să se simuleze (prin stabilirea regulilor de tranziție) toți ceilalți executori, realizând într-un fel procesul de calculare pas cu pas, în care fiecare etapă a calculului este destul de elementară.
Pe mașina Turing, puteți simula mașina Postului. algoritmii normali Markov și orice program pentru computerele obișnuite care convertesc datele de intrare în ieșire printr-un algoritm. La rândul său, pe diferiți artiști abstracți, este posibil să imităm mașina Turing. Interpreții, pentru care acest lucru este posibil, se numesc Turing complet (Turing complete).
Există programe pentru computerele obișnuite care simulează funcționarea mașinii Turing. Dar trebuie remarcat faptul că simularea nu este completă, deoarece există o mașină Turing Rezumat bandă fără sfârșit. O bandă fără sfârșit cu datele imposibil de a simula pe deplin pe un calculator cu o memorie finită (memoria totală de calculator - RAM, hard disk-uri, diverse externe medii de stocare, registre, și memoria cache CPU, etc -. Fii foarte mare, dar, cu toate acestea, întotdeauna este finit).
Opțiunile mașinii Turing [editați] edita wiki-text]
Modelul mașinii Turing permite extensii. Puteți lua în considerare mașinile Turing cu un număr arbitrar de benzi și benzi multidimensionale cu constrângeri diferite. Cu toate acestea, toate aceste mașini sunt Turing complete și modelate de o mașină convențională Turing.
Mașina Turing care lucrează pe o bandă semi-infinită [edit] edita wiki-text]
Un exemplu de astfel de informații, luați în considerare următoarea teoremă: Pentru orice mașină Turing există o mașină Turing echivalentă care funcționează pe o bandă de semi-infinit (care este, pe bandă, fără sfârșit de sens).
Luați în considerare dovada dată de Yu G. Karpov în cartea Theory of Automata. Dovada acestei teoreme este constructivă, adică dăm un algoritm prin care o mașină Turing echivalentă cu proprietatea declarată poate fi construită pentru orice mașină Turing. În primul rând, numărăm în mod arbitrar celulele MT de bandă de lucru, adică definim noua locație a informațiilor de pe bandă:
Apoi renumerotăm celulele și presupunem că simbolul "*" nu este conținut în dicționarul MT:
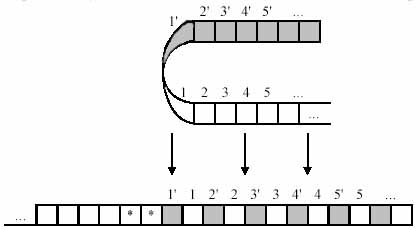
În cele din urmă, schimbați aparatul Turing, dublarea numărului statelor sale, și de a schimba trecerea de cap de citire-scriere, astfel încât un grup de statut mașină ar fi echivalentă cu activitatea sa în zona umbrită, în timp ce celălalt grup a mașinii de stat ar lucra ca lucrările de mașini originale într-o zonă neimpozată. În cazul în care MT se va întâlni caracterul „*“, apoi capul de citire-scriere a ajuns în zona de frontieră:
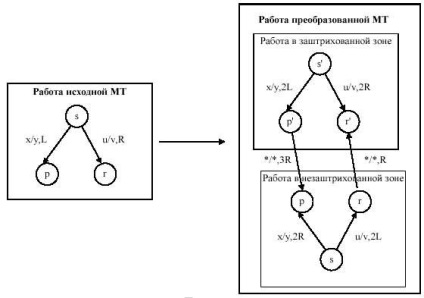
Starea inițială a noii mașini Turing este setată în una sau în cealaltă zonă, în funcție de locul în care a fost așezat capul de citire-scriere în configurația originală în care parte a benzii sursă. Evident, caseta din stânga a marcatorilor de restricție "*" nu este utilizată într-o mașină Turing echivalentă.
Două-dimensională mașini Turing [edita] edita wiki-text]
Vezi și [editați] edita wiki-text]
Alți artiști abstracți și sisteme formale de calcul [edit] edita wiki-text]
Note [editați] edita wiki-text]
3. O mașină de stat finită - Un automat de stare finită sau automată de stare finită, automat finit sau pur și simplu o mașină de stat, este un model matematic de calcul. Este o mașină care poate fi găsită într-un număr finit de state. FSM se poate schimba de la o stare la alta ca răspuns la intrările externe. Un FSM este definit de o listă a statelor sale. Comportamentul mașinilor poate fi observat în multe dispozitive din societatea modernă pe care le prezintă. Mașina de stat finită are mai puțină putere decât alte modele de calcul, cum ar fi mașina Turing. Distincția de putere computațională înseamnă că există sarcini pe care le poate face o mașină Turing. Acest lucru se datorează faptului că FSM-urile sunt studiate în domeniul mai general al teoriei automate. Un exemplu de mecanism care poate fi modelat de o mașină este un turnichet. Un turnichet, folosit pentru a accesa metrou și plimbări cu parc de distracții, este o poartă cu trei brațe rotative la înălțimea taliei, una peste intrare. Inițial brațele sunt blocate, blocând intrarea, împiedicând patronii să treacă, depunând o monedă sau un jeton în slotul de pe turnicheți. După ce clientul trece, brațele sunt blocate, blocate, blocate, din nou. Există două intrări care îi afectează starea, punând o monedă în slot și împingând brațul. În starea blocată, împingerea brațului nu are efect, indiferent de câte ori este de intrare. În starea deblocată, punerea în circulație a monedelor suplimentare nu are nici un efect, însă un client care împinge brațele, dând o intrare împingă, schimbă starea înapoi la Blocat. Fiecare stat este reprezentat de un nod, marginile arată tranzițiile de la o stare la alta. Fiecare săgeată este etichetată cu intrarea care declanșează acea tranziție, o intrare care nu provoacă o schimbare a stării este reprezentată de o săgeată circulară revenind la starea inițială. Săgeata în nodul blocat de la punct indică faptul că este starea inițială