În cazul în care integrand este înlocuit de un polinom interpolare, atunci vom obŃine formulele de cvadratură ale formei:
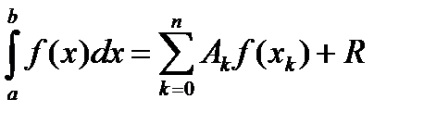
unde xk sunt nodurile de interpolare selectate; Ak sunt coeficienți care depind de nodurile selectate, dar nu depind de forma funcției f (x); R este termenul restul care determină eroarea maximă atunci când se utilizează formula de cvadratură; k = 0, 1, ..., n.
Prin divizarea segmentului de integrare [a, b] în n părți egale de un sistem de puncte
și calcularea integrand în nodurile rezultate
se obțin formulele de cvadratură pentru nodurile echidistante. Aceste formule sunt numite formulele Newton-Cotes. Cele mai convenabile pentru integrarea numerică sunt polinomii de interpolare cu ordine scăzută, prin care se obțin formule compuse destul de simple.
Formula trapezului se obține în cazul utilizării polinomului de interpolare de ordinul întâi:
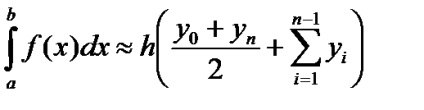
Termenul rămas are forma: Folosind formula trapezoidală la calcularea unui integru definit duce la o eroare în care
Pentru a găsi valoarea aproximativă a unui integral integrat, folosind formula trapezoidală, se poate folosi algoritmul, schema acestuia fiind prezentată în Fig. 5.5.
Eroarea restricției pentru metoda trapezoidală este mai mare decât pentru alte formule Newton-Cotes, dar atractivitatea acesteia constă într-o simplă implementare. În plus, o ușoară complicație a algoritmului face posibilă reducerea semnificativă a erorii de calcul, astfel încât formula trapezoidală este adesea utilizată (în combinație cu alte formule).
De exemplu, în cazul aproximării integrantei prin polinomul de interpolare Hermite, formula lui Euler este obținută:
Termenul rest al acestei formule indică faptul că o mică adăugare la formula trapezoidală crește în mod substanțial precizia sa.
În ultima formulă, valorile derivatelor pot fi înlocuite cu diferențe bidimensionale
Ca rezultat, formula lui Euler se transformă în formula lui Grigorie. Dar ordinea generală a preciziei va scădea de la al patrulea la al treilea.
(2) Formula pentru parabole (Simpson)
Folosind polinomul de interpolare de ordinul doi (parabola) obținem formula de integrare numerică - formula lui Simpson:
Fig. 5.5 Algoritmul pentru calculul unui integral definit de formula trapezoidală
În Fig. 5.6 prezintă schema algoritmului care realizează calcule folosind formula parabolică. Atunci când formula este implementată, numărul de noduri este neapărat ciudat, adică numărul de secțiuni ale partiției din intervalul de integrare trebuie să fie uniform: n = 2m. Algoritmul folosește o tehnică în care numărul repetărilor unui ciclu este redus la jumătate, adică modificarea parametrului ciclului este efectuată de două ori, ceea ce reduce timpul de execuție al algoritmului. Metoda Simpson este considerată a fi una dintre cele mai utilizate metode de integrare numerică, care oferă o precizie destul de bună a calculelor.
Fig. 5.6 Algoritmul pentru calculul unui integral integral folosind formula Simpson
(3) Formula lui Newton (regula de trei optzeci)
O precizie mai mare a calculului asigură interpolarea integrandului printr-un polinom de gradul trei. Rezultatul este formula lui Newton (regula de trei optzeci):
Schema algoritmului de integrare numerică prin regula de trei optzeci este prezentată în Fig. 5.7 Formulele Newton-Cotes, a patra, a cincea și a șasea au găsit și aplicații practice, dar utilizarea lor conduce la scheme mai greoaie.
Fig. 5.7 Algoritmul pentru calculul unui integral integral prin formula lui Newton