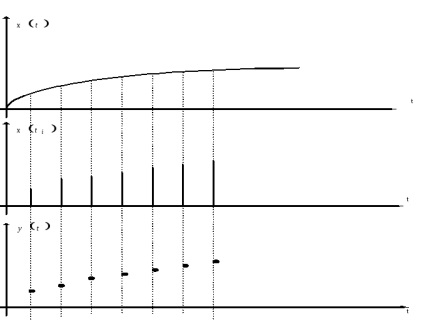
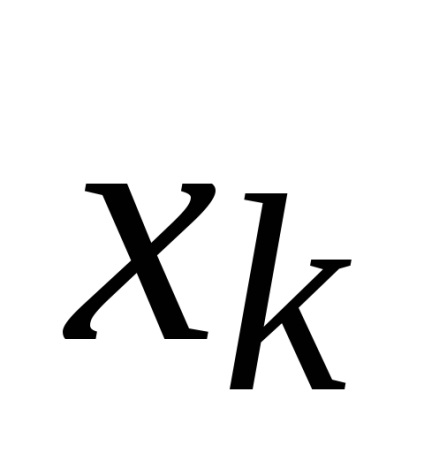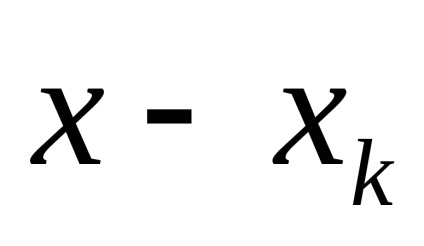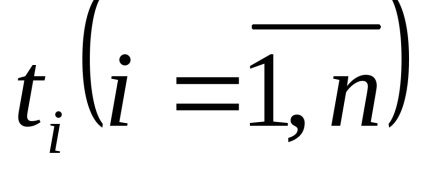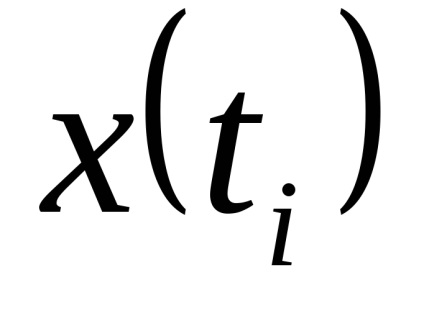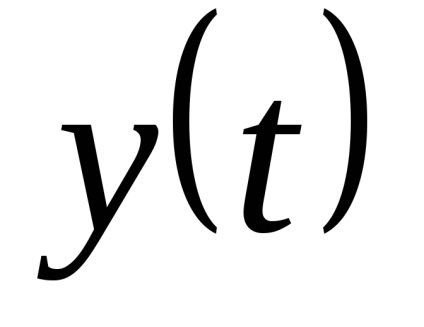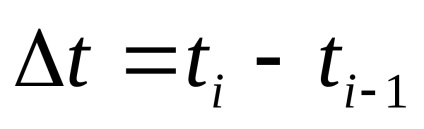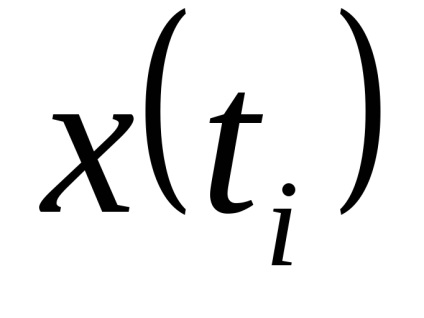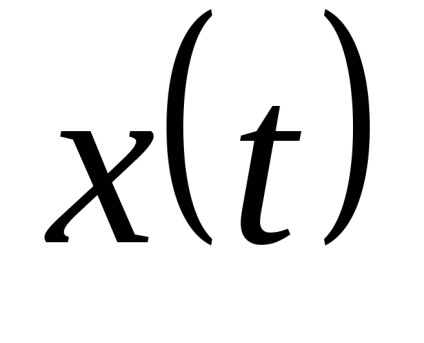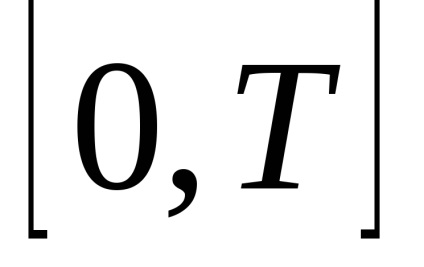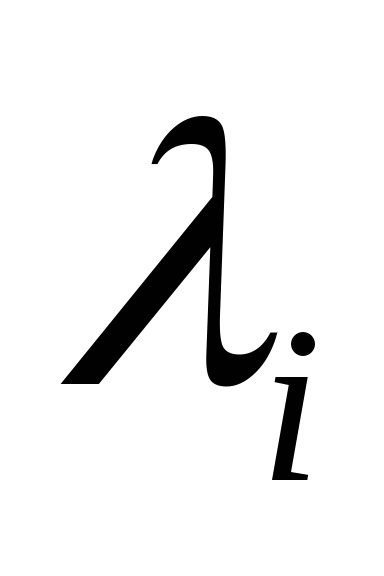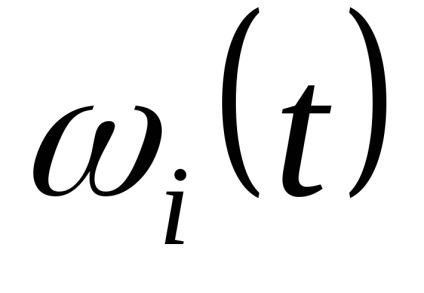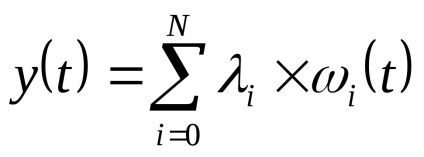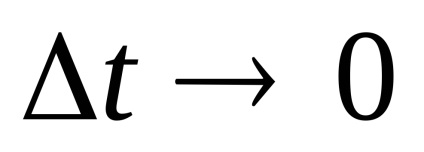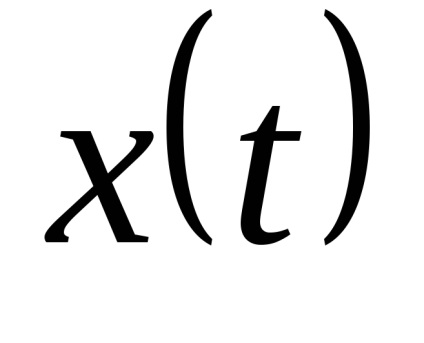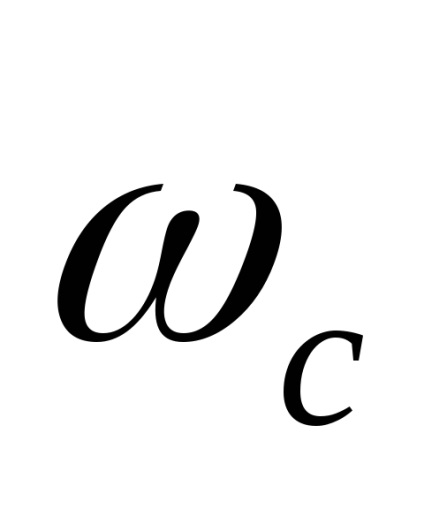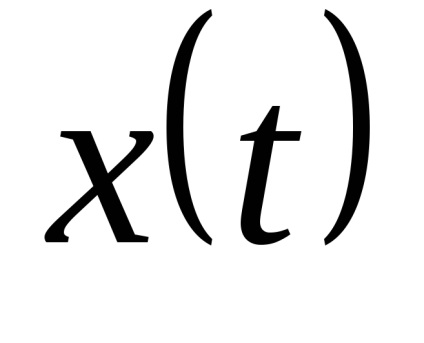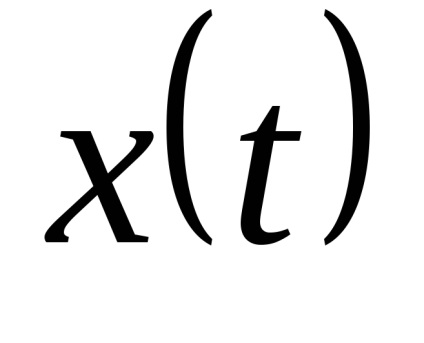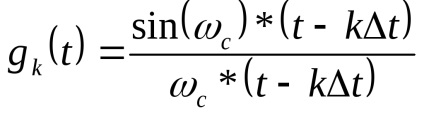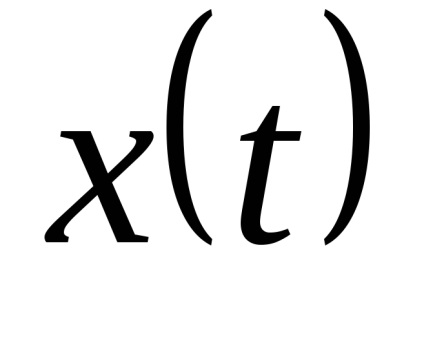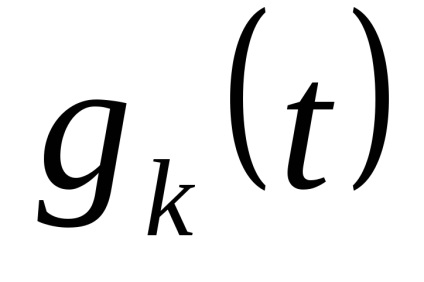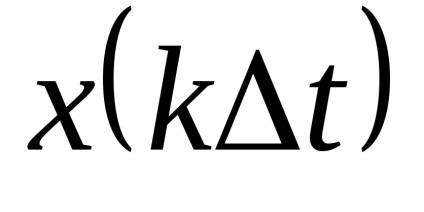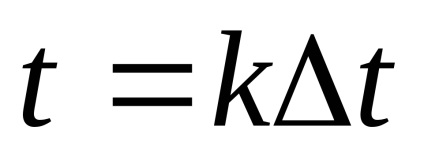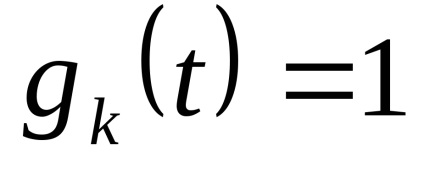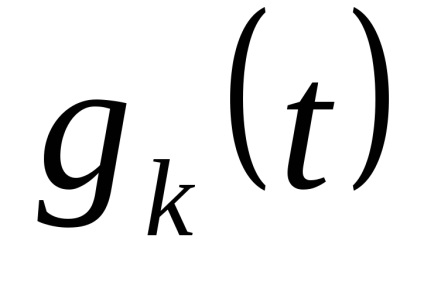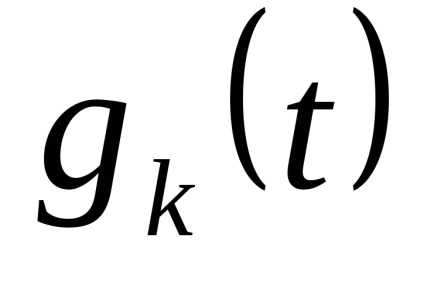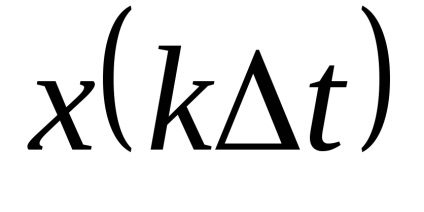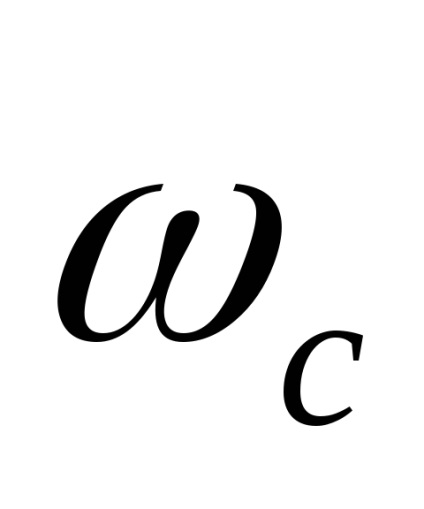Legea distribuției x și x este aleatorie. Ca nivele de cuantizare, cel mai bine este să luați midpoints din segmentele partiției. (Arată!)
În funcție de metoda de transformare, ISP-urile sunt împărțite în dispozitive de conversie directe și de echilibrare.
Nu există feedback general în conversia directă ЦИП. Acestea au o viteză foarte mare, dar acuratețea lor este ridicată doar la o precizie ridicată a tuturor convertoarelor.
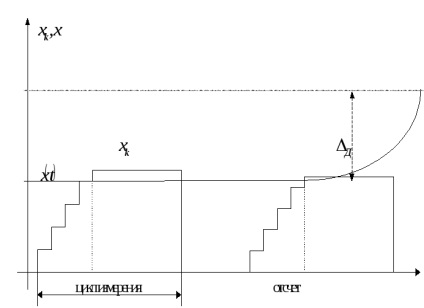
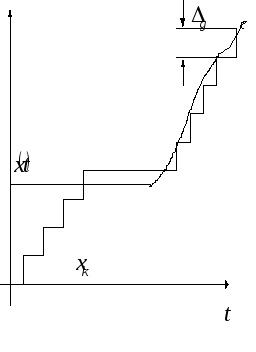
Transformarea de echilibrare ЦИП este acoperită de un feedback comun. Convertorul de feedback DAC al semnalului de ieșire discret în cantitatea compensatoare xk de o natură fizică cu valoarea măsurată x (t). DAC este fabricat din elemente de înaltă precizie și stabilitate.
Există dispozitive care implementează și urmăresc echilibrarea.
Pentru prima etapă, valoarea cantității compensatorii
în fiecare ciclu de măsurare crește de la zero la pași egali cu pasul de cuantificare. Când se ajunge la egalitate, procesul de echilibrare se oprește și rezultatul măsurătorii egal cu numărul de pași de cuantificare a cantității compensatorii este fixat. Citirea se face de obicei la sfârșitul ciclului.
Apare o eroare dinamică.
În
dispozitivele de compensare de urmărire nu readuc nivelul de compensare la zero, ci rămân constante. Când schimbați x, este monitorizat lanu a depășit valoarea etapei de cuantificare. Numărarea se efectuează fie în momentul echilibrării, fie prin comenzi externe. Acest lucru este mult mai dificil din punct de vedere tehnic.
6.3. Eșantionarea timpului și restaurarea funcțiilor continue.
Există mai multe modalități de eșantionare.
Trecerea de la funcția de timp continuă la funcția de timp discret poate fi realizată prin prelevarea probelor de funcții la anumite momente discrete ale timpului
. Pe baza conteazăputeți restabili o altă funcție (cea pe care o căutați), reproducând originalul cu o precizie dată. Când este discretizat în timp, una dintre cele mai importante este chestiunea alegerii pasului de discretizare:
.
Există o etapă optimă de eșantionare care asigură restaurarea funcției inițiale cu o precizie specificată, cu un număr minim de eșantioane pe un interval de timp finit.
Funcție continuă
la intervalele de observarese înlocuiește cu un număr finit de coeficienți de expansiuneasupra sistemului ales de funcții de bază
Convenabilitatea acestui sistem.
Se poate presupune că restabilirea exactă a funcției continue inițiale în timp este posibilă numai cu
. Cu toate acestea, există o clasă largă de procese pentru care recuperarea exactă este posibilă la o rată de eșantionare finită. Această clasă include semnale cu un spectru limitat.
6.3.1. Teorema lui Kotelnikov.
Dacă funcția continuă
îndeplinește condițiile Dirichlet (limitată, continuu pe o parte și are un număr finit de extreme), iar spectrul său este limitat de o frecvență(frecvența cutoff), atunci există un astfel de interval minimîntre numărătoare, în care este posibilă reconstrucția corectă a unei funcții discretizabilepe contează discret. Acest interval maxim:
O teoremă privind posibilitatea extinderii funcției
într-un rând:
funcția numărătoare (6.7)
Ie funcție
poate fi extins în termeni de sistem de funcții de bază. Mai mult decât atât, coeficienții de expansiunela momente discrete ale timpului.
la
valoare maximă
funcții
sunt ortogonale pe un interval de timp infinit de mare.
Valoarea practică a extinderii funcției în seria Kotel'nikov este aceea că canalele de comunicare cunoscute nu sunt transmise canalului de comunicare
, dar sunt transmise numai funcțiile lattice.
Din punct de vedere al implementării practice, funcția de numărare corespunde în totalitate variației timpului în tensiunea de ieșire a unui filtru ideal de trecere inferioară care trece în mod egal toate frecvențele de la 0 la
, când a fost depus la intrarea luiimpulsa.
În condiții reale, reconstrucția exactă este imposibilă, deoarece condițiile teoremei Kotelnikov nu sunt îndeplinite.
Funcția reală
pe intervale de timp finite, astfel încât spectrele lor sunt infinite.
Articole similare