În unele mecanisme, este destul de simplu să se construiască un plan al pozițiilor mecanismului. Astfel de mecanisme includ mecanismul articulației cu patru articulații articulate.
Selectați factorul de scală al lungimii
și se calculează toate lungimile din secțiunile desenului.
Se construiește o poziție arbitrară a mecanismului. Luăm un punct arbitrar A. față de care se determină poziția punctului D. Radii AB și CD poartă cercuri (traiectoriile punctelor B și C). Dintr-un punct arbitrar B al cercului AB, raza BC este o crestătură pe cercul CD. În acest caz, două puncte C și C 'se pot întoarce (nu sunt prezentate în figură). Alegeți una care corespunde schemei date, în acest caz punctul C. Puncte A. În. C și D sunt conectate prin linii drepte, se obține o poziție arbitrară a mecanismului (în figură este prezentată prin linii subțiri).
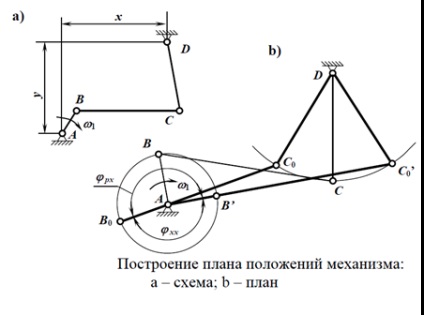
Pozițiile extreme ale balansierului sunt determinate: cea dreaptă se obține atunci când manivelul AB și tija de legătură BC sunt întinse de-a lungul unei linii, în condițiile AC = AB + BC. Poziția din stânga a basculantului va fi atunci când manivelul AB și tija de conectare BC se extind de-a lungul unei linii, dar cu AC = BC - AB. Două puncte B (B 0 și B ') și două puncte C (C 0 și C') sunt obținute. Pentru o anumită direcție a vitezei unghiulare a manivelei, punctul B ar trebui luat ca începutul cursei de lucru. deoarece, cu proiectarea corectă a mecanismului, unghiul pârghiei la cursa de lucru # 61546; px ar trebui să fie mai mare decât unghiul de ralanti.
Pornind de la punctul B, un cerc de rază AB este împărțit de-a lungul direcției de rotație a pârghiei cu numărul necesar de segmente (6, 8 sau 12) și se obține numărul corespunzător de poziții de manivelă. Din punctele B 1. B 2, etc. raza aeronavei pe traiectoria punctului C al rocker-ului este făcută cu crestături, obține puncte C 1. C 2 etc. care sunt conectate cu punctele corespunzătoare din B și cu punctul D și se obține numărul necesar de poziții ale mecanismului.