Metode de specificare a grafurilor:
Stabiliți un grafic folosind o matrice de incidență
nm - unde n este numărul de vârfuri ale graficului, m este numărul de muchii ale graficului. Vitezele și marginile indică vârfuri și muchii, iar la intersecția i-rândului și coloanei j, dacă marginea i este incidentă cu vârful j, am setat 1 și 0 în caz contrar.
În cazul unui digraph
Orice alt număr este atribuit în buclă. (de obicei 2)
Lista marginilor graficului
Lista de margini a graficului reprezintă. coloană. În coloana din stânga, toate margini sunt enumerate, iar nodurile care le sunt incadrate, iar pentru n-graf ordinea de scriere a nodurilor este arbitrară, iar pentru orografie numărul primei arc este primul.
Dacă graficul are vârfuri izolate, acestea sunt plasate la sfârșitul listei.
O matrice de adjuvant este o matrice pătrată de dimensiune, unde n este numărul de vârfuri ale graficului.
În cazul unui n-graf, numărul de muchii care leagă aceste două noduri este fix.
În cazul unei ortograme, se pune numărul de arce care au un început la vârf și un capăt la vârf.
Definiția 2.21. Matricea de adjuvantitate a unui grafic finit G cu vârfuri p este matricea A (G) = || aij || (i, j = 1, 2, ..., p), în care dacă nodurile sunt adiacente, setăm 1, altfel 0.
42. Acțiuni pe grafice.
Un grafic H va fi numit o parte a graficului G (G) dacă setul V (H) și numeroasele margini E (H) sunt cuprinse în punctele corespunzătoare pentru graficul G: u.
Un grafic H se numește un graf sigraph G dacă face parte din graficul G, iar numărul de vârfuri ale graficului H este egal cu numărul de vârfuri ale graficului G, adică V (H) = V (G).
Un grafic G (G) se numește subgraful grafic al lui G (V) dacă graficul G (G) conține toate marginile care intră în contact cu vârfurile MNV.
Definim câteva operații pe grafice:
Ștergeți sau adăugați o margine.
Îndepărtarea vârfului. Din mulțimea de vârfuri, ștergeți vertexul selectat și din setul de margini toate margini care se încadrează în el.
Împingerea coastei. Identificăm (contracte) vârfuri care se încadrează în marginea aleasă.
Adăugarea unui vârf (partiție margine). Alegem o muchie (u, v) din setul de muchii și o eliminăm. Adăugați un nou punct vertex w la mulțimea de vârfuri și adăugați margini noi (u, w) și (w, v) la setul de margini.
Adăugarea părții H a graficului G este. grafic care satisface traseul. condiţii:
43. Grafice orientate și nedirecționate.
Un grafic G este o colecție de 2 seturi (V, E), unde V este setul de vârfuri ale graficului, iar E este setul de margini ale graficului. Între vârfurile și marginile graficului G, relația de incidență este stabilită. Se consideră că o margine este incidentă la noduri, dacă conectează aceste două noduri. Mai mult, vârfurile sunt numite adiacente. Relația de incidență este cel mai important element al graficului; indică modul de combinare a seturilor V și E într-un singur obiect. Dacă o margine care unește două vârfuri este direcționată de la un vârf la altul, atunci se numește orientat sau arc și este grafic reprezentat de săgeți direcționate de la început până la sfârșit. Un grafic care conține arce este numit direcție sau digraf. Un grafic care nu conține nici un arc (care conține numai margini) este numit un nod sau n-graf.
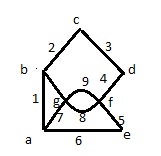
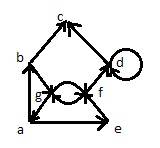
H-GRAPH (Figura 1) OR-GRAF (Fig.2)
Marginile care intră în aceeași pereche de vârfuri sunt numite multiple (în fig.1 acestea sunt marginile de la 8 și 9).