Fracțiunea obișnuită Fracțiunea ca urmare a împărțirii numerelor naturale.

3 Calculați mod convenabil: - · 16 + 16 · 60 + 33 · 22-69 · 22 = = 120 = 16 · (23 + 77) = 1,600 = = 130 = 60 · (67 + 33) = 6000 = 22 · (79-69) = 220

4 Efectuați acțiunile și exprimați dividendul printr-un coeficient incomplet, divizorul și restul: 1. 75. 185 75 = 9 · 8 + 3 48 = 17 · = 500 · = 185 · 2

5 O bucată de fir de 1 m lungime a fost tăiată în 2 părți egale. Care este lungimea unei bucăți. 1 m. Exprimați lungimea firului în decimetri: 1 m = 10 dm. Apoi 10: 2 = 5 (dm). Răspuns: 5 dm lungime dintr-o bucată.

6 O bucată de fir de 1 m lungime a fost tăiată în 3 părți egale. Care este lungimea unei bucăți. 1 m 1 m 1 m = 10 dm; 10: 3 = 3 (ost 1); 1 m = 100 cm, 100: 3 = 33 (ost 1); 1 m = 1000 mm; 1000: 333 = 3 (ost 1);

7 Amintiți-vă cum să citiți fracția înregistrată? Amintiți-vă cum să citiți fracția înregistrată? O treime Care este numărul de deasupra liniei de fracții? Care este numele numărului de deasupra liniei fracției? Numerator Care este numele numărului de sub bara? Care este numele numelui sub bară? Numitorul Ce înseamnă linia bordură? Ce înseamnă linia bordură? Acțiunea de divizare

8 unu - 1-numerotator al treilea - 3 - numitor unu - 1 - numărător al treilea 3 - numitor Amintește-ți cum să citești fracțiunea înregistrată? Amintiți-vă cum să citiți fracția înregistrată? O treime Care este numărul de deasupra liniei de fracții? Care este numele numărului de deasupra liniei fracției? Numerator Care este numele numărului de sub bara? Care este numele numelui sub bară? Numitorul Ce înseamnă linia bordură? Ce înseamnă linia bordură? Acțiunea de divizare

9 O bucată de fir de 1 m lungime a fost tăiată în 3 părți egale. Care este lungimea unei bucăți. 1 m 1 m Soluție: Răspuns: contor. 1. 3 = 1 3 (m)

10 O bucată de fir de 3 m lungime a fost tăiată în 7 părți egale. Care este lungimea unei bucăți. 3 m
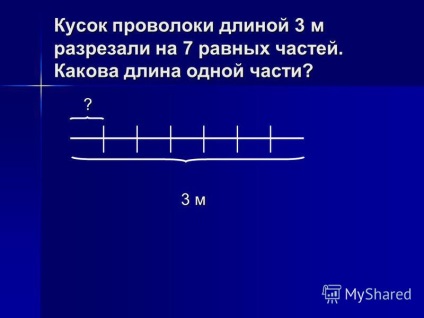
11 O bucată de fir de 3 m lungime a fost tăiată în 7 părți egale. Care este lungimea unei bucăți. 3 m Soluție: Răspuns: lungimea contorului este o piesă. 3: 7 = 3 (m) 7
Fracțiunea obișnuită Fracția ca rezultat al împărțirii numerelor naturale.

13 Câmpul divizării numerelor naturale poate fi scris sub forma unei fracții. Numerotatorul unei fracții este un dividend, iar numitorul este un divizor. 1: 3 = 1 și 3: 7 = 3 37
14 Motivul numerelor naturale m si n poate fi scris sub forma unei fractiuni, unde numarul m este multiplu, numitorul este n-divizor. m n

15 Cum se citește fracțiunea: "em en" "em en" "împărțită la n" "împărțită la n" (abrevierea n este permisă). m n
16 Din istoria fracțiunilor Necesitatea unor măsurători mai precise ale cantităților a dus la faptul că unitățile de măsură au fost împărțite în mai multe părți egale: 2.4.8, etc. Fiecare parte a măsurătorii inițiale a primit propriul nume. De exemplu, jumătate din Rusia antică a fost numită încă - jumătate, aproximativ a patra parte au spus - a patra, în cea de-a opta parte - o jumătate de oră, în jurul celei de a șaisprezecea - o jumătate de bucată. Părți echivalente ale întregii măsuri au fost denumite acțiuni: acțiuni a patra, opt, etc.
17 Din istoria fracțiunilor Un sistem interesant de măsuri a fost în Roma antică. Ea se baza pe împărțirea vechii unități romane de masă, numită ACC. Ass au fost împărțite în 12 părți egale. Cea de-a douăsprezecea parte a eseului a fost numită o uncie. În timp, uncii au fost folosiți pentru a măsura alte cantități. De exemplu, un roman putea spune că a trecut peste 7 uncii de cale. În acest caz, desigur, nu a fost vorba despre cântărirea drumului. Sa înțeles că au trecut șapte "doisprezece" din drum.
18 Din istoria fracțiilor la Roma în cursul au fost doar 18 fracțiuni diferite: „Produse semi-fabricate“ - jumătate asul, „SEKSTANS“ - al șaselea din cota sa, „SEKSTANS“ - al șaselea din cota sa, „SESKUNTSIYA“ - al optulea, „triens“ - un al treilea asul, "BES" - două treimi, "Seminium" - jumătate de uncie. "BES" - două treimi, "Seminium" - jumătate de uncie. Triens SESTANS + = Semi BES · Reguli SESKUNTSIYA = OZ au fost atât de multe încât capacitatea de a opera cu fracții percepute ca un miracol. De aceea, întotdeauna și peste tot cunoașterea fracțiunilor era percepută ca un miracol.
19 Din istoria fracțiunilor În faimosul său "Aritmetic", un matematician rus al secolului al XVIII-lea, L. F. Magnitsky, a scris: "Dar nu ai acea aritmetică, Întreg în tot inculpatul, Și în acțiuni este nesemnificativ. Același lucru despre tine, Budi, în părți pe care le știi. "
20 Scrieți sub forma unei fracții, care parte a figurinei este umbrită:
21 Determinați care parte din figură este umbroasă în gri. Încercați să oferiți mai multe răspunsuri.
22 Câmpul numerelor naturale m și n poate fi scris sub forma unei fracții, unde numitorul m este un multiplu, iar numitorul este n-divizorul. m n
23 Tema: 1. p. 19 (p. 86). Înregistrează în notebook (în, d) Una din problemele vechi.
24 Probleme Vintage care implică fracții 1. Obiectivul de „aritmetică“ celebru secolul Asia Centrală Matematică IX 1. Obiectivul „aritmetică“ celebru secolul central din Asia Matematica IX, Muhammad Ibn Musa al-Khwarizmi (sarcina este prezentată într-o versiune simplificată): „Găsiți numărul, știind că dacă iei o treime și un sfert din ea, primești 10 "
25 Sarcina Vintage 2. Sarcină cu fracții de la „Papirusul Rhind“ 2. Problema „Papirusul Rhind“ (Egipt 1850 BC) (Egipt 1850 BC) „vine cu 70 oier tauri. El este întrebat: - Cât de mult îți aduceți cireada voastră numeroasă? Păstorul răspunde: aduc două treimi din o treime din vite. Citiți-o. "
26 Probleme Vintage care implică fracții 3. King sarcină indian 3. problema indian King (matematica secolul Sriddihary XI.) Există Kadamba petale de flori, pe de o cincime din albine a coborât. În apropiere a crescut imediat în floare de Simengda Și pe ea a treia parte se potrivesc. Diferența pe care le găsiți, de trei ori ei și albinele pe Kuta plantate, doar două nu au găsit un loc oriunde, toate zboară înainte și înapoi, și peste tot parfumul florilor de a se bucura. Sună-mă acum Numărătoare în minte, câți albine s-au adunat aici?
27 problemă Vintage cu fracții 4. Provocarea om de știință armean Ananias Shirakatsy 4. Provocarea om de știință armean Ananias Shirakatsy (secolul VII î.Hr.). (Secolul VII d.Hr.). „Un comerciant a trecut prin 3 orașe, și obținut de la el în primul oraș, și taxa pe jumătate și o treime din proprietate, iar în a doua jumătate a orașului și a treia (cu ceea ce este stânga), iar al treilea oraș din jumătate și al treilea (cu ceea ce a mai rămas ). Când a ajuns acasă, avea 11 bani (unități monetare). Deci, aflați cât de mulți bani erau la început de la comerciant.