o undă care diferă radial de (convergând) la o anumită axă într-un spațiu sau punct pe un plan. În ultimul caz, aceste valuri sunt numite. de asemenea, circulară. Exemple de ts. pot servi ca valuri pe suprafața apei dintr-o piatră abandonată sau un plutitor oscilant, electromagnet. sau acustică. valuri excitate de surse situate într-un spațiu, limitat, de exemplu. două reflectoare plane plane (inclusiv, ghiduri de undă oceanice etc.).
Structura cc Este mult mai complicat decât structura plane (unidimensională) și sferică. (tridimensionale). Cel mai simplu monocrom. simetrice c.c. cu o sursă în centru (Figura 1) satisface o ecuație de undă bidimensională și este descrisă cu ajutorul funcției Hankel de ordin zero H0 (kr):
unde ω este frecvența circulară, k este numărul de undă. La distanțe mari de la axă (kr -> 1), câmpul de undă (1) are forma:
u (r, t) = (A / r) exp (wt-kr), (2)
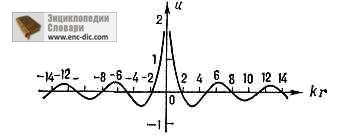
Fig. 1 Cilindric divergent radial. val excitat de o sursă în centru.
și numai în acest asimptotic. reprezentare în Ts. poate identifica în mod unic amplitudinea A / r și faza wt-kr = w (t-r / vph), în care vp viteza de fază coincide cu faza a vitezei undei plane: vp = w / k = 2p / l (lungimea de undă l-). Deoarece distanța de la axa pătratului modulului undei perturbație (2) descrește ca 1 / r, iar suprafața cilindrului care acoperă creșterile sursa proporțional cu r, astfel că, în conformitate cu legea de conservare a energiei, valoarea totală a fluxului de energie transportate mai departe de sursa de pe o axă, rămâne constantă. In absenta dispersiei undelor armonice. valuri (2) de pe axa poate crea un val de orice formă (în particular, solitar val sau val pachet), se deplasează cu o viteză constantă vp = v
unde funcția f (t - r / v) satisface ecuația unidimensională a undelor. Cu toate acestea, în regiunea intermediară, unde kr = 1,
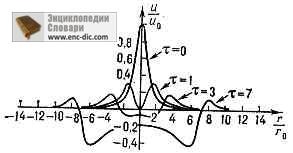
Fig. 2. Cilindric divergent radial. un val dat la momentul inițial al timpului sub forma unui singur impuls u = u0 / (1 + r / r0) 3/2. Cu creșterea t = ct / r0 (cu creșterea timpului t), impulsul se răspândește, lăsând în urmă o "traseu".
chiar și fără un mediu de dispersie puternic val de deformare perturbația (Fig. 2). Acest lucru se datorează faptului că Ts. în principiu, nu staționare: se deplasează departe de axa (centru), își rezervă „coada“ de a-ing ar putea fi interpretată ca rezultat sosirea perturbațiilor val din ce în ce mai mult de la distanță dintr-un punct de observație pe axa sursei.
Ajutor pentru motoarele de căutare