Suprapunerea forțelor electrostatice
Din legea lui Coulomb și din convenție, că atracția sau respingerea electrostatică este o forță (prin urmare, ea poate fi descrisă de un vector), urmează o regulă despre ce trebuie făcut în cazul a trei sau mai multe acuzații. Să presupunem că doriți să determinați forța care acționează asupra celei de-a treia încărcări de celelalte două încărcări (Figura 274).
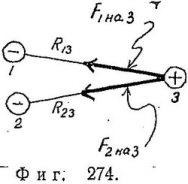
Cu ajutorul legii Coulomb, este posibil să se determine forțele cu care prima și a doua sarcină acționează asupra celei de-a treia (în fig. 274, aceste forțe sunt notate F1, respectiv cu 3 și F2 cu 3). Forța totală aplicată celei de-a treia încărcări este egală cu suma vectorilor acestor forțe. Aceasta este cea mai importantă proprietate a forțelor electrice (și forțele gravitaționale), constând în faptul că forța de interacțiune a două încărcături nu se schimbă în prezența celei de-a treia, a patra sau a celei de-a cincea sarcini. Aceasta ne permite să determinăm efectul unui întreg sistem de taxe asupra oricărei alte taxe prin adăugarea directă a efectelor încărcărilor individuale ale sistemului.
Un exemplu. Care este forța interacțiunii a două sarcini în 5 e. Art. u și 25 el. Art. u situate la o distanță de 10 cm unul față de celălalt?
Dacă ambele încărcări sunt pozitive, forța va fi respingătoare. Același lucru se poate spune despre două taxe negative (de aici este vizibilă convenția numelor "pozitive" și "negative"). Dacă, pe de altă parte, o taxă este negativă, iar cealaltă este pozitivă (de exemplu, 5 e, și 25 e., Sau 5 e, și 25 e, unități), pentru fiecare încărcare Forța de atracție în 1,25 dynes va acționa.
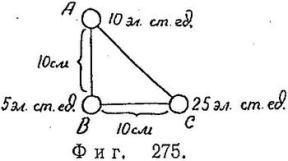
Să presupunem că am introdus oa treia încărcare, așa cum se arată în Fig. 275. Întrebarea este: care sunt componentele orizontale și verticale ale forței care acționează asupra încărcăturii B?
Încărcarea C exercită o acțiune (direcționată spre stânga) pe încărcarea B. Încărcarea este de 10 e. Art. u (A) respinge și sarcina B, dar această forță este îndreptată în jos. Valoarea sa este:
Foriz = 1,25 dynes (direcționat spre stânga),
Fwerth = 0,5 dyne (direcționat în jos). (19,8)
Introducerea unui câmp electric
Conceptul câmpului, pe care îl vom introduce acum, ar putea fi determinat și în cazul forțelor gravitaționale. Apare atunci când încercați să descrieți forța care acționează asupra unei încărcări la un anumit punct din spațiu din partea multor alte sarcini și atribuie acestui punct al spațiului o anumită proprietate care afectează mișcarea particulelor. Am fost de acord că forța care acționează asupra încărcării punctului de la alte încărcări este egală cu suma vectorială a forțelor pe partea încărcărilor individuale. În cazul celor trei sarcini discutate mai sus, a treia sarcină este acționată de forță:
Mărimea și semnul forței F1 la 3 sunt determinate de formula:
și magnitudinea și semnul forței F2 cu 3 - conform formulei:
Fiecare dintre aceste expresii conține factorul q3; acest lucru rezultă direct din legea lui Coulomb. În cazul în care ar exista taxe N, suma vectorială ar consta în termeni N, toate cantitățile din care ar fi proporționale cu tariful de la punctul 3.
Acest lucru face posibilă aplicarea unei tehnici care pare trivială pentru a ajunge la conceptul de câmp electric. Luăm factorul q3 din expresia forței și introducem o nouă valoare a lui E:
Această cantitate, adică vectorul E1 cu 3, numim câmpul electric, care excită încărcarea 1 la punctul 3. Rețineți că magnitudinea câmpului electric nu depinde de existența oricărei încărcări în punctul 3. Mai mult, rezultatul electric câmpul de la punctul 3 este egal cu suma vectorilor câmpurilor electrice create de fiecare încărcare a sistemului; pe baza acestui fapt, putem introduce câmpul electric total la punctul 3:
În sistemul GHS, câmpul electric este măsurat în dyne / el. Art. u taxa.
Nu este surprinzător, dacă pare incomprehensibil, pentru care era necesar să se introducă o valoare suplimentară. Faraday a introdus-o pentru prima dată pentru a face mai vizibil efectul unor acuzații asupra altora. Maxwell a încercat să reprezinte câmpul electric ca o tensiune mecanică în eter. De atunci, valoarea câmpului electric sa răspândit cu mult peste orice interpretare mecanică. Odată cu concepte precum impulsul sau energia, câmpul electric a început să joace un rol mai important decât teoriile private din care s-au născut aceste concepte. În acest sens, vom fi convinși când studiem radiațiile electromagnetice.

Câmpul electric poate fi numit funcție vectorială. Un vector este conectat cu fiecare punct al spațiului, iar acest vector, înmulțit cu încărcătura, dă valoarea forței care acționează asupra acestei încărcări la un anumit punct din partea încărcărilor care creează câmpul. Dacă cunoaștem câmpul electric în toate punctele din spațiu, înseamnă că știm forța care va acționa asupra încărcăturii în orice moment, chiar dacă nu știm ce sistem de sarcini care a creat acest câmp este 1). Aceasta este principala conveniență a conceptului introdus; în unele cazuri, este mai ușor să operezi cu un câmp existent decât cu particulele încărcate care îl creează.
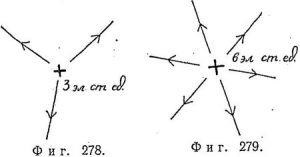
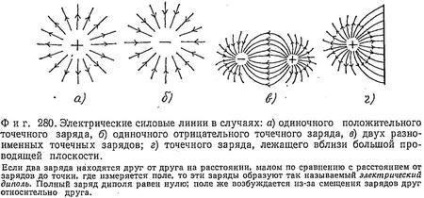
Câmpul electric este greu de imaginat în figură, deoarece pentru acest lucru în fiecare punct al spațiului este necesar să se deseneze un vector. Totuși, este posibil să se tragă vectori numai în anumite puncte din spațiu, cum ar fi, de exemplu, în Fig. 277, care arată câmpul electric al unei încărcări punctuale pozitive. Lungimile vectorilor scad cu distanta ca 1 / r 2 si toate sunt dirijate radial din sarcina. Uneori, pentru claritate, nu sunt trase vectori, ci linii solide care sunt peste tot paralele cu câmpul la punctele prin care trec aceste linii. Amploarea câmpului este caracterizată de densitatea liniilor. De exemplu, putem fi de acord că de la o taxă de 1 e. Art. u trebuie să existe o linie. Apoi, de la o taxă de 3 e. Art. u vor ieși 3 linii de forță, și din sarcina de 6 e. Art. Există șase linii, așa cum se arată în Fig. 278 și 279 (vezi de asemenea fig.280).
1) Se presupune că introducerea unei noi taxe nu încalcă distribuirea inițială a tarifelor pentru care a fost găsit un câmp.
În Fig. 281 prezintă liniile de forță ale câmpului electric de două plăci, diferite de cele încărcate (un astfel de sistem se numește capacitate sau un condensator). Cu excepția marginilor, densitatea liniilor electrice de forță între plăci este constantă. Același lucru este valabil și pentru magnitudinea și direcția câmpului electric corespunzător.
Uneori se întâmplă ca obiectele mici să fie aliniate paralel cu câmpul electric, dacă sunt create condițiile necesare. Destul de ciudat, dar așa se comportă semințele de iarbă, suspendate într-un lichid neconductor. (De ce se întâmplă acest lucru?) Dacă vom crea un câmp electric într-un astfel de fluid, prin imersarea corpurilor încărcate în el, semințele se vor alinia de-a lungul direcției câmpului și vom putea observa modelul liniilor de forță formate de aceste semințe. În ciuda atracției externe a unor astfel de tablouri, ele sunt destul de înșelătoare, deoarece pot crea impresia eronată că liniile de forță există într-adevăr.
Rezumând cele de mai sus, afirmăm că câmpul electric este o funcție vectorială a coordonatelor spațiale (la fiecare punct al spațiului care corespunde unui vector), determinat de distribuția încărcărilor. Dacă în orice punct din spațiu punem o sarcină q care nu încalcă distribuția inițială a sarcinilor, atunci forța va fi acționată de forță:
Astfel, cunoscând câmpul electric, suntem capabili să determinăm forța aplicată încărcării în orice punct al spațiului, chiar dacă nu știm distribuția de sarcină care generează câmpul (figura 282).
Întrebarea este: cum putem găsi un câmp electric dacă este dată o distribuție de taxe? În cazuri simple, putem folosi legea lui Coulomb și apoi rezumăm contribuțiile din toate taxele. Pentru cazuri mai complexe care implică o distribuție arbitrară a taxelor, s-au dezvoltat metode foarte elegante. Plecând de la legea Coulomb, este posibil să se obțină câteva teoreme puternice care permit să se determine câmpurile simplu și rapid în cazul distribuțiilor relativ complexe, dar simetrice. Cu toate acestea, nu ne interesează aceste metode, deci nu le vom descrie aici.