p.1.1 Conceptul de vector
Multe cantități fizice, de exemplu, forța, deplasarea unui punct material, viteza, sunt caracterizate nu numai prin valoarea lor numerică, ci și prin direcția în plan sau în spațiu. Astfel de cantități fizice se numesc cantități vectoriale (sau vectori scurt).
Să luăm în considerare un exemplu. Lăsați forța în SH să acționeze asupra corpului. În figură, această forță este reprezentată de un segment cu o săgeată (figura 1). Săgeata indică direcția forței aplicate, iar lungimea segmentului corespunde valorii numerice a forței în scala aleasă.
Dispărând de la proprietățile specifice ale cantităților vectoriale fizice, ajungem la conceptul geometric al unui vector.
Luați în considerare un segment arbitrar. Pe aceasta puteți specifica două direcții: de la un capăt la altul și viceversa (figura 1).
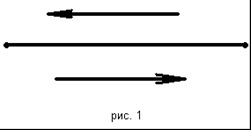
Pentru a alege una dintre direcții, un capăt al segmentului este numit începutul. iar celălalt - sfârșitul și vom presupune că segmentul este direcționat de la început până la sfârșit.
Definiție: O pistă, pentru care se indică care dintre capetele sale este considerată a fi începutul și care este sfârșitul, se numește un segment sau un vector direcționat.
În figuri, vectorul este reprezentat de un segment cu o săgeată care indică direcția vectorului. Vectorii sunt marcate cu două litere latine litere mari, cu o săgeată deasupra lor, de exemplu. Prima literă indică începutul vectorului, al doilea indică sfârșitul (figura 2).
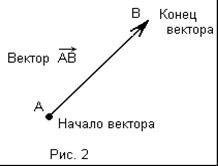
Figura 3a prezintă vectorii
; punctul - începutul acestor vectori și - sfârșitul lor. Vectorii sunt adesea denotați de o literă latină cu litere mici, cu o săgeată deasupra ei: (fig.3, b).

Pentru viitor, se recomandă să fie de acord că orice punct al avionului este, de asemenea, un vector. În acest caz, vectorul este numit zero. Originea vectorului zero coincide cu capătul său, în figură un astfel de vector este reprezentat de un singur punct. Dacă, de exemplu, punctul reprezentând vectorul zero este desemnat de litera M, vectorul dat poate fi desemnat (figura 3, a). Vectorul zero este de asemenea indicat de simbol. În figura 3, a este nenul, iar vectorul este zero.
Lungimea sau modulul unui vector nonzero este lungimea segmentului AB. Lungimea vectorului (vector) este notată după cum urmează. Lungimea vectorului zero este considerată egală cu zero.
Egalitatea vectorilor
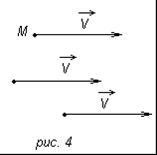
Înainte de a da o definiție a vectorilor egali, să ne uităm la un exemplu. Să considerăm mișcarea unui corp în care toate punctele sale se mișcă cu aceeași viteză și în aceeași direcție. Viteza fiecărui punct M al corpului este o cantitate vectorică, deci poate fi reprezentată de un segment direcționat al cărui origine coincide cu punctul M (figura 4). Deoarece toate punctele corpului se mișcă cu aceeași viteză, toate segmentele direcționate reprezentând vitezele acestor puncte au aceeași direcție, iar lungimile lor sunt egale.
Acest exemplu ne spune cum să determinăm egalitatea vectorilor. Conceptul de vectori coliniari este introdus preliminar.
Definirea vectorilor non-zero sunt numiți coliniari dacă se află pe o linie sau pe linii paralele; Vectorul zero este considerat colinar cu orice vector.
Dacă doi vectori nonzero sunt coliniari, atunci ele pot fi direcționate fie identic fie opuse. Acești vectori sunt numiți respectiv direcționați în mod co-direcțional și îndreptat opus, folosind următoarea notație:
Originea vectorului zero coincide cu capătul său, deci vectorul zero nu are o direcție definită. Cu alte cuvinte, orice direcție poate fi considerată direcția vectorului zero. Am acceptat să presupunem că vectorul zero este co-direcționat cu orice vector.
Acum, pe baza celor de mai sus, este ușor să se dea o definiție a vectorilor egali.
Definiția. Vectorii sunt numiți egali dacă sunt co-directionați și lungimile lor sunt egale.
§1.3 Depunerea unui vector dintr-un anumit punct
Dacă punctul A este începutul vectorului. atunci ei spun că vectorul este eliberat din punctul A (figura 5). Se confirmă următoarea afirmație:
Din orice punct al M putem amâna un vector egal cu un vector dat. și astfel numai unul.
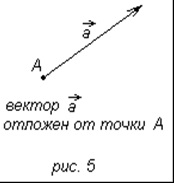
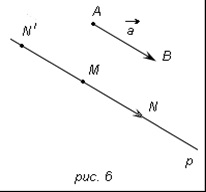
De fapt, dacă este un vector zero, atunci vectorul este vectorul necesar. Să presupunem că vectorul este diferit de zero, iar punctele A și B sunt începutul și sfârșitul lui. Tragem prin punctul M linia p. paralel cu AB (fig.6) (dacă M este un punct al liniei AB, atunci pentru linia dreaptă p luăm linia dreaptă AB în sine). Pe linia p amângem segmentele MN și. egală cu segmentul AB. și alegeți din vectori cel care este co-direcțional cu vectorul (în figura 6 vectorul). Acest vector u este vectorul dorit egal cu vectorul. Merită acordată atenție concluziei cu privire la unicitatea unui astfel de vector: o astfel de concluzie se face pe baza cifrei.
Notă. Vectorii egali amânați din diferite puncte sunt adesea denotați de aceeași literă. De exemplu, sunt indicate vectorii de viteză egali ai diferitelor puncte din Figura 4. Uneori, acești vectori sunt considerați a fi același vector, dar sunt amânați din diferite puncte.
Du-te la descărcarea fișierului