Figura 2.2 arată cum particulele oscilează în valuri longitudinale și transversale.
Undele longitudinale și transversale care se propagă într-un mediu semibond se numesc valuri de volum.
Vitezele undelor longitudinale și transversale se calculează după cum urmează:
- viteza undei longitudinale (12)
și coeficienții Lamei, (13)
E este modulul de elasticitate de primul fel, # 961; - densitatea, - raportul lui Poisson.
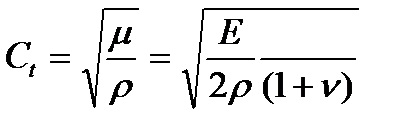
la # 957; = 0.3 obținem
Viteza undelor longitudinale este Cl = 5900 m / s, viteza undei transversale este Ct = 3200 m / s.
Unda transversală poate avea o polarizare diferită.
Dacă planul de polarizare este perpendicular pe reflector, atunci astfel de valuri transversale sunt numite valuri SV.
Dacă vectorul vitezei vibraționale este paralel cu planul reflectorului, atunci astfel de valuri sunt numite valuri SH. Același val, în funcție de orientarea planului reflectorului, poate fi polarizat în raport cu acesta, SV sau SN. În Fig. 3.1. polarizat în planul desenului este un transversal val val SV de fund plan D perpendicular pe planul desenului și vectorul viteză oscilatorie. În același timp, este un val SH pentru planul B paralel cu vectorul de viteză vibratoare.
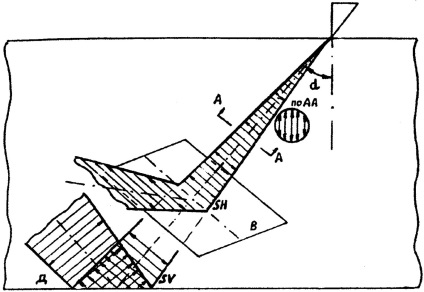
Fig. reflexie 3.1 Schema de unda transversala polarizată liniar este excitat de sonda înclinat planul B (Sn polarizare) și planul inferior L (SV-polarizare)
Coeficientul de reflexie al undelor transversale depinde puternic de orientarea planului de polarizare față de reflector.
Când se utilizează oscilațiile SV-val al căror plan se află în planul desenului (în planul de incidență), ceea ce este tipic pentru sonda convențională câmp oblic, semnalul de reflexie R variază așa cum se arată în figura 3.2. linie solidă. Dacă planul oscilațiilor este ortogonal față de planul de incidență (unde SH), atunci este independent de # 946; R = 1.
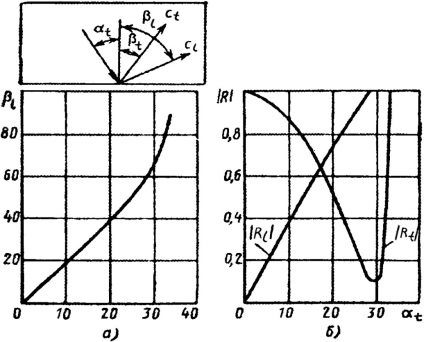
Figura 3.2. Unghiurile dependente (A) și coeficientul de reflexie R (b) al unghiului # 945; t.
În propagarea de valuri de orice natură, ei (valurile) suferă amortizare, adică amplitudinea scade cu distanța de la punctul de excitație al undei. Coeficientul de atenuare este compus din coeficienții de împrăștiere # 948; p și absorbție # 948; etc e. # 948; = # 948; n + # 948; p.
Atunci când energia sonoră absorbită este transformată în căldură, dar în împrăștierea rămâne sunet, dar lasă valurile de înmulțire napravlenno care rezultă din reflecțiile dar limitele granulei și neomogenitatilor.

Fig. 3.3. Imprastierea undelor ultrasonice intr-un metal.
Absorbția sunetului în solide se datorează în principal fricțiunii interne și conductivității termice. Absorbția undelor transversale este mai mică decât valurile longitudinale, deoarece acestea nu sunt legate de schimbările adiabatice în volum, la care apar pierderile de conductivitate termică. Coeficientul de absorbție în substanțele solide este proporțional cu ƒ (sticlă, țesuturi biologice, metale) sau ƒ2 (cauciuc, materiale plastice).
În cristale unice, atenuarea este determinată de absorbția undelor ultrasonice. Metalele utilizate în practică au o structură policristalină și, în mod obișnuit, atenuarea ultrasunetelor este determinată în primul rând de împrăștiere. În cristale, viteza sunetului are o valoare diferită în funcție de direcția propagării sale în raport cu axele de simetrie ale cristalului. Acest fenomen se numește anizotropie elastică.
Într-un metal, cristalele sunt orientate în moduri diferite, astfel încât atunci când ultrasunetele se schimbă de la un cristal la altul, viteza sunetului poate varia într-o măsură mai mare sau mai mică. Ca urmare, apar reflecția parțială, refracția și transformarea ultrasunetelor, ceea ce provoacă mecanismul de împrăștiere (Figura 3.3).
Un efect mare asupra coeficientului de dispersie în metale este raportul D (dimensiunea medie a granulelor) și lungimea de undă cu ultrasunete # 955;
VARIATII # 955; < Mai ales mare este atenuarea ultrasunetelor la # 955; ≈ (2,4) D. Aici, pentru a difuza împrăștierea, se adaugă absorbția. NA ric.3.4. Este arătată atenuarea undelor transversale și longitudinale în funcție de frecvență. la (8. 10) D, ultrasunetele cu granulație mică sunt împrăștiate și coeficientul # 948; este proporțională cu Dƒ4 (împrăștiere Rayleigh). Cu 4D ≤ # 955; ≤ 10D, coeficientul de atenuare este proporțional cu produsul Dƒ2. Cel mai mic amortizare va fi # 955; ≥ (20,100) D. Dacă această condiție este îndeplinită, atunci puteți controla produsele cu o grosime de 8. 10m. valoare # 948; determină în mare măsură frecvența vibrațiilor cu ultrasunete. Pe de o parte, pe măsură ce frecvența crește, amplitudinea semnalului crește datorită îmbunătățirii directivității radiației și, pe de altă parte, amplitudinea semnalului scade din cauza creșterii atenuării.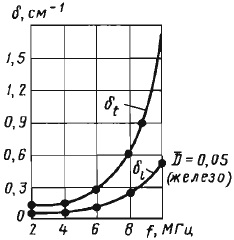
Fig. 3.4. Atenuarea undelor transversale și longitudinale în funcție de frecvență.
Un fenomen fizic important în defectoscopie este difracția undelor ultrasonice. Difracția în mediile elastice diferă brusc de difracția obișnuită, de exemplu, din difracția luminii.
Difracția este înțeleasă ca procesele care apar atunci când undele ultrasonice se întâlnesc cu obstacole. Valul, întâmpinând un obstacol în cursul propagării în spațiu, variază în amplitudine și în fază și, penetrând în regiunea umbrei, se abate de la calea rectilinie. În acest caz, comportamentul câmpurilor de unde nu respectă legile optice geometrice (raze). Luați în considerare modelul de difracție pentru defecte plane (fig.3.5) și vrac (fig.3.7).
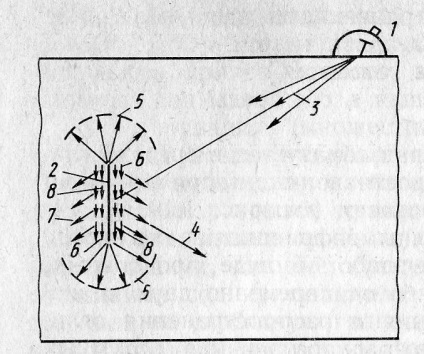
Figura 3.5. Difracția pe un defect plat: convertor 1; 2-defect; Val 3-incident; 4-reflectat; 5-margine, 6-cap; 7-lateral transversal; 8 suprafață.
Liniile de undă se formează atunci când razele cad pe o margine ascuțită. La incidență oblică a unui val de excitat pe valuri de frontieră de difracție crăpătură închise în unghiul conului de care este egală cu de două ori unghiul de incidență la marginea. Undele de graniță au o față sferică. Pe margine există două tipuri de valuri de margine: longitudinale și transversale. Amplitudinea semnalelor de difracție este semnificativ (cu 20-30 dB) mai mică decât amplitudinea semnalelor de la undele care le generează. Excepția este semnale ale căror direcții coincid cu direcția semnalului care a atins marginea crack-ului. Amplitudinea undelor de forfecare difracționată rămâne practic constantă în domeniul de unghiuri # 945; = 10 ÷ 60 de grade. (Figura 3.6).
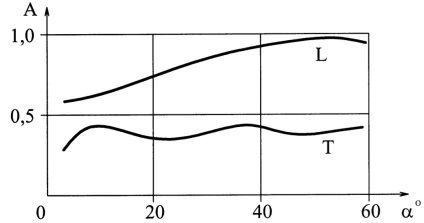
Fig.3.6. Raportul dintre amplitudinile undelor de margine difracționate și un defect plat.
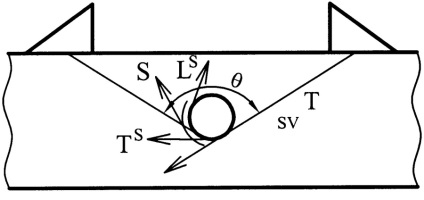
Figura 3.7. Difracția unui val transversal printr-un defect de volum.
Când valul cade pe o suprafață circulară (pori), se formează un câmp de împrăștiere din undele reflectate, plicuri și alunecări (figura 3.7).
Valul de îndoire (alunecare) poate fi de trei tipuri: # 955;, T, S - tipuri. Razele valului T incident, care ating suprafața cilindrului, excită un val de suprafață alunecător de tip transversal (TS). Razele care apar pe suprafața la cel de-al treilea unghi critic generează un val alunecător de tip longitudinal (# 955; S). Un val alunecător de tip Rayleigh (S) este excitat de grinzile adânci care trec lângă suprafață în direcția tangentei. O estimare a energiilor fiecărui val arată că pentru cele mici # 952; Cea mai mare energie are un val de tip Rayleigh. Odată cu creșterea # 952; amplitudinea valului de forfecare alunecător crește. Acest lucru se datorează faptului că valul transversal este excitat mai eficient, dar se descompune mai puternic. Prin urmare, determină semnalul difracționat numai la unghiuri mari de cotitură # 952; când calea care trece prin ele scade (figura 3.8).
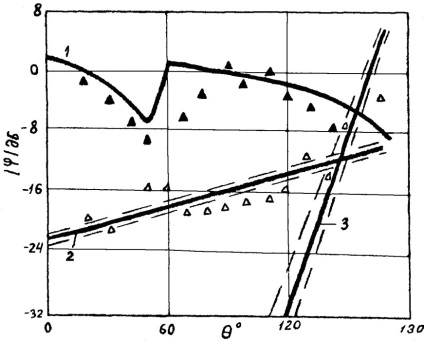
Fig. 3.8. Amplitudinea semnalelor împrăștiate pe cilindru cu un diametru de 6 mm; 1 - semnalul reflectat în oglindă; 2,3 - semnale re-emise de valurile de alunecare de tip Rayleigh și transversale.
Această condiție este cel mai adesea observată cu o schemă combinată de control, atunci când unghiul # 952; este maximă. Sa stabilit experimental că odată cu scăderea dimensiunii (R) înconjoară reflectorul mărește amplitudinea semnalului difractate (ADIF) (ris.3.9). Viteza undelor plicului depinde, de asemenea, de dimensiunea undei defectului () (figura 3.10).
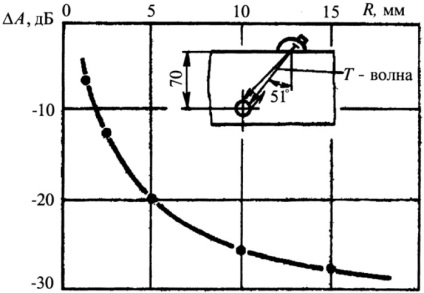
Ris.3.9. Dependența amplitudinilor semnalului reflectorizant și difracționat la dimensiunile reflectorului de volum.
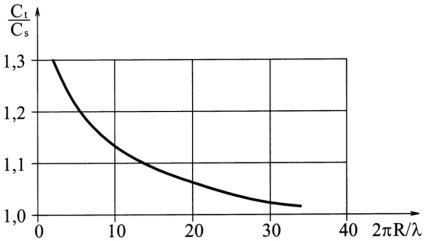
Ris.3.10. Dependența vitezei valului difracționat de dimensiunea defectului.