Ecuații diferențiale și sisteme de ecuații
Pentru a rezolva ecuații și sisteme diferențiale în Matlab oferă următoarea funcție ode45 (f, interval, X0 [, options]), ode23 (f, interval, X0 [, opțiuni]), ode113 (f, interval, X0 [, opțiuni]), odel5s (f, interval, X0 [, opțiuni]), ode23s (f, interval, X0 [, optiuni]), ode23t (f, interval, X0 [, optiuni]) si ode23tb (f, interval, X0 [, opțiuni] ).
Parametrii de intrare ai acestor funcții sunt:
- f este o funcție vectorală pentru calcularea părții drepte a ecuației sistemului de ecuații
- interval - o matrice de două numere care definește intervalul de integrare a unei ecuații sau a unui sistem diferențial;
- X0 este un vector al condițiilor inițiale ale unui sistem de sisteme diferențiale
- opțiuni - parametrii de control pentru soluția unei ecuații sau a unui sistem diferențial.
Toate funcțiile se întorc:
- array T - coordonatele nodurilor de rețea în care se dorește soluția;
- matricea X a cărei coloană i este valoarea vectorului-vector de soluție la nodul Ti
În ode45 funcții metoda de Runge-Kutta 4-5 ordine de precizie implementate în ode23 funcții sunt puse în aplicare, de asemenea, metoda Runge-Kutta, dar ordinea de 2-3, și funcția ode113 implementează metoda Adams.
În fișierul M cu numele pr 7. m scriem:
Apoi, în fereastra de comandă numim ode113:
Rezultatul este un grafic:
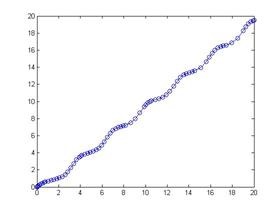
Este necesar să se implementeze metoda Runge-Kutta a ordinului 4 și să se rezolve problema Cauchy pentru sistemul propus de ecuații diferențiale:
În fișierul M cu numele pr 8. m scriem:
Apoi, în fereastra de comandă, sunăm funcția ode 45:
[x, y] = ode45 (@ pr8, [1 10], [0,1 0,5]);