2. Afirmația problemei
6. Construirea unei soluții generale prin metoda matricei
7. Problema Cauchy pentru metoda matricei
Să considerăm un sistem de ecuații liniare de ordinul întâi, scrise în formă normală:
unde coeficienții aij. i = 1,2, .... n, k = 1,2, ..., n, sunt valori constante;
yi = yi (t), i = 1,2, ..., n sunt funcții necunoscute ale variabilei t.
Dacă setăm bi (t) (i = 1,2, ..., n) egal cu zero (bi (t) = 0), atunci obținem un sistem omogen corespunzător sistemului neomogen (1).
Denumind matricea sistemului cu A (x) și vectorul
Apoi, sistemul (1) poate fi rescris în formă de matrice
, atunci obținem sistemul corespunzător de ecuații omogene
Fiecare colecție de funcții n
definit și continuabil diferențiat în intervalul (a; b), se numește o soluție a sistemului (1) în acest interval dacă inversează toate ecuațiile sistemului (1) în identități:
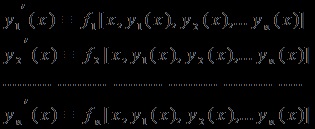
sunt valabile pentru toate valorile lui x în intervalul (a, b). Soluția generală a sistemului neomogen este suma soluției generale a sistemului omogen corespunzător, iar soluția particulară este neomogenă.
2. Afirmația problemei
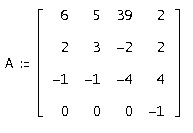
Obiectiv: să studiem metodele de rezolvare a unui sistem de ecuații diferențiale cu o matrice constantă:
;
;
1. Găsiți valorile proprii și construiți un sistem fundamental de soluții (FSS).
2. Construiți o matrice fundamentală prin metoda Euler.
3. Găsiți soluția aproximativă sub forma unei serii de matrice.
4. Construiți o soluție generală prin metoda matricei. Pentru a investiga dependența formei Iordaniei a matricei A de valorile proprii.
5. Rezolva problema Cauchy.
Vectorul condițiilor inițiale: [1, 2, 3, 4]
Un sistem liniar omogen de ecuații diferențiale este un sistem de ecuații de formă:
Dacă este în matricea sistemului
= const, atunci acest sistem se numește un sistem cu coeficienți constanți sau cu o matrice constantă.
Sistemul fundamental al soluțiilor unui sistem liniar omogen de ecuații este baza spațiului liniar al soluțiilor a, adică n soluții lineare independente ale acestui sistem.
Pentru a construi un sistem fundamental de soluții de ecuații diferențiale necesare pentru a găsi valorile proprii ale polinomului caracteristic, deoarece, în funcție de tipul lor (numerele caracteristice pot fi foarte diferite, multiple, complex) a construit un sistem fundamental de soluții.
Pentru ca acest sistem de n ecuații omogene lineare cu n necunoscute să aibă o soluție netrivială, este necesar și suficient ca determinantul sistemului (Wronskian) să fie egal cu zero:
Din această ecuație a gradului n, valoarea k este determinată, pentru care sistemul are soluții netriviale. Ecuația (4) se numește caracteristică.
Se scrie un polinom caracteristic, pentru aceasta folosim funcția CHARPOLY
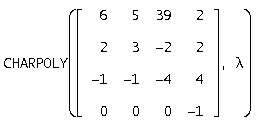
Pentru a gasi valorile proprii, folosim functia SOLVE (U, l), care returneaza numerele caracteristice ale matricei A vectorului l. Avem:
S-au dovedit două rădăcini
și două rădăcini complexe conjugate
. În consecință, vectorii care formează matricea fundamentală pentru acest tip de rădăcini vor fi separați pentru
. Să scriem FSS pentru datele pentru numerele caracteristice obținute:
Matricea y (x), ale cărei coloane reprezintă soluțiile care formează sistemul fundamental, se numește matrice fundamentală.
Iar soluția generală a sistemului va arăta astfel:
Să găsim soluția acestui sistem folosind metoda Euler.
Metoda Euler este după cum urmează.
Soluția sistemului (1) este în forma:
Funcția (5) este o soluție a sistemului (1) dacă
Este valoarea proprie a matricei A și a este vectorul propriu al acestei matrici care corespunde numărului
. Dacă valorile proprii
matricile A sunt pereche distincte și a1. a2. ..., a sunt vectorii proprii corespunzători ai acestei matrici, atunci soluția generală a sistemului de ecuații (1) este definită de formula:
În cazul rădăcinilor multiple, soluția sistemului ia forma
unde Pi (x) sunt polinoame de grad nu mai mare de (k-1) avand in totalitate coeficienti arbitrari. Deci, printre coeficienții acestor polinomi, coeficienții sunt arbitrari, iar restul k · n-k sunt exprimați prin ei. Pentru a găsi coeficienții polinomilor, înlocuim soluția (6) în sistemul inițial de ecuații, echivalând coeficienții pentru aceleași funcții. Rezolvăm sistemul cu privire la coeficienții (k · n-k). Obținem expresia tuturor coeficienților în termeni de coeficienți liberi.
Dacă este pentru o valoare mai mare de eigen
matricea A există cât mai multe vectori proprii liniar independenți
, care este multiplicitatea sa, atunci ea corespunde soluțiilor independente k ale sistemului original:
Dacă este pentru o valoare proprie
de multiplicitate k există numai m (m , poate fi căutat sub forma unui produs al unui polinom vector cu gradul k - m Pentru a găsi vectori , Este necesară înlocuirea expresiei (4) în sistem (3). Ecuând coeficienții acestor termeni în părțile stângi și drepte ale sistemului, obținem o ecuație pentru găsirea vectorilor . Au fost găsite următoarele valori proprii pentru această sarcină: . Am construit un sistem fundamental de soluții: Gasim un rand al matricei fundamentale de solutii pentru numarul caracteristic . Scriem a treia linie de soluții într-o formă generală:
În cazul în care aij se găsește prin expresia:
Exponentul e A al matricei A este suma seriei
unde E este matricea identității.
Proprietatea exponentului matricei:
a) dacă AB = BA, atunci e A + B = e A * e B = e B * e A;
b) atunci când A = S - 1 * B * S, adică, A = S -1 * e * B S, unde matricea S - este o matrice de transformare a bazei variabilelor eigenbasis în variabilele originale.
c) matricea y (t) = e At este o soluție a matricei Problema Cauchy:
și anume este matricea fundamentală a sistemului (1).
Din proprietatea c) rezultă că soluția y (t) a sistemului (1) satisface condiția y (0) = y0. este determinată de expresia y (t) = e At * y0. Astfel, problema găsirii soluțiilor sistemului de ecuații (1) este echivalentă cu problema găsirii matricei eAt de matricea A.
Pentru a calcula matricea e At, este convenabil să reprezentăm matricea A sub forma:
,
unde matricea S este matricea transformării variabilelor de la eigenbasis la baza variabilelor inițiale, iar BA este forma Jordan a matricei A, deoarece e At = S -1 * e Bt * S.
Forma Iordaniei a matricei depinde de tipul de numere caracteristice.
1. Să presupunem că numerele caracteristice sunt multiple multiple, atunci forma Jordan a matricei dimensiunii nxn are forma:
- adevărata rădăcină a multiplicității n.
2. Dacă printre rădăcinile unui polinom caracteristic există ambele rădăcini reale diferite și reale, atunci matricea B are forma:
- adevărate rădăcini diferite și
- adevărata rădăcină a multiplicității 2.
3. Dacă există printre rădăcinile polinomului caracteristic al rădăcinilor complexului conjugat Iordania, celula arată astfel:
complexă rădăcină conjugată a polinomului caracteristic.
Deoarece în cazul nostru printre numerele caracteristice sunt prezente rădăcinile complexe conjugate n = 2 - # 59329; ∨ l = 2 + # 59329; și rădăcinile reale diferite n = -1 ∨ n = 1, atunci matricea Jordan arată astfel:
Din ecuația S = A * S * V, unde S - matrice non-singular, obținem un sistem de ordinul 16, din care găsim elementele matricei S. Matricea rezultată S este după cum urmează:
Rezolvăm sistemul ordinii 16 din ecuația A * S = S * B

Definim unele elemente și obținem următoarea matrice S:
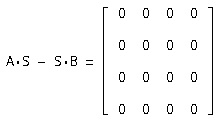
Deci, matricea de tranziție se găsește corect.
Pentru a găsi vectorul de soluție y, multiplicați matricea S cu
- este un vector ale cărui elemente depind de rădăcinile polinomului caracteristic:
Pentru numere complexe
are următoarea formă:
În cazul rădăcinilor reale diferite:
=
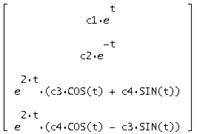
De aici găsim soluția generală y = S *
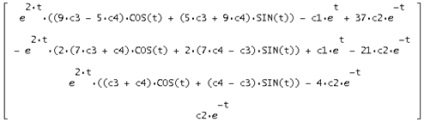
Atunci când soluția este înlocuită în sistemul inițial, se obține egalitatea corectă, ceea ce înseamnă că soluția se dovedește a fi corectă:
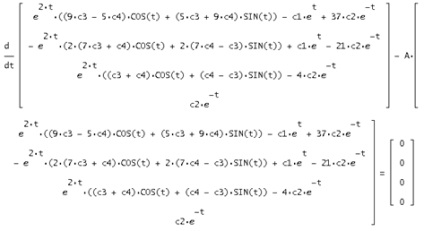
7. Problema Cauchy pentru metoda matricei
Este necesar din toate soluțiile sistemului de ecuații să găsească o soluție în care y (i) (t) ia o valoare numerică dată y0i la un anumit punct, adică găsiți valorile lui ci pentru următoarele valori date: x = 0, y = [1, 2, 3,4].
În vectorul de soluție y (t) înlocuim condițiile date și soluționăm sistemul obținut în raport cu c1, c2, c3, c4:
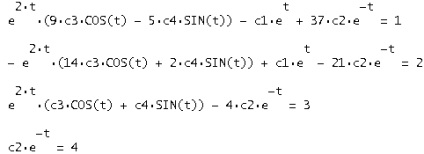
Ca rezultat, obținem:
Substituind c1, c2, c3, c4 în soluția generală, obținem o soluție în forma Cauchy:
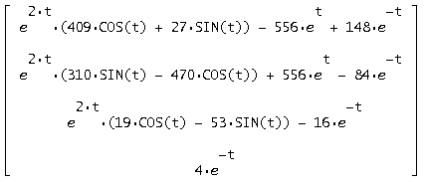
:

Vectorul zero rezultat
. În consecință, matricea găsită este o soluție a sistemului original.
Fie J blocul Jordan al matricei A. Pentru cazul rădăcinilor reale diferite, blocul Jordan va arăta astfel:
Să presupunem că între valorile proprii reale ale matricei A sunt multiple. Celula Iordan va fi în conformitate cu următoarea formulă:
De exemplu, dacă multiplicitatea este k = 2, atunci putem scrie celula matricei Jordan după cum urmează:
Dacă multiplicitatea este k = 3, atunci putem scrie celula matricei Jordan după cum urmează:
Dacă între cele trei valori proprii
sunt rădăcini de multiplicitate 2, atunci formularul Jordan va arăta astfel:
Dacă două valori proprii ale matricei A sunt conjugate complexe, atunci intrarea celulei Iordan va arăta astfel:
Este partea imaginară a eigenvaluei
.
Soluția generală a sistemului neomogen poate fi găsită prin formula: