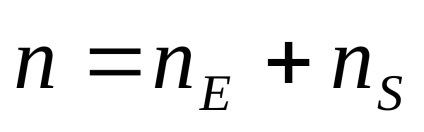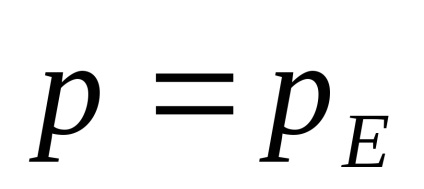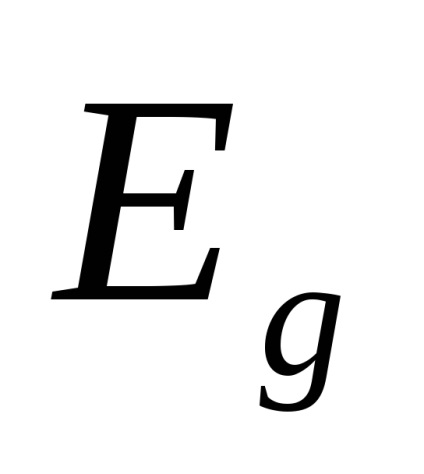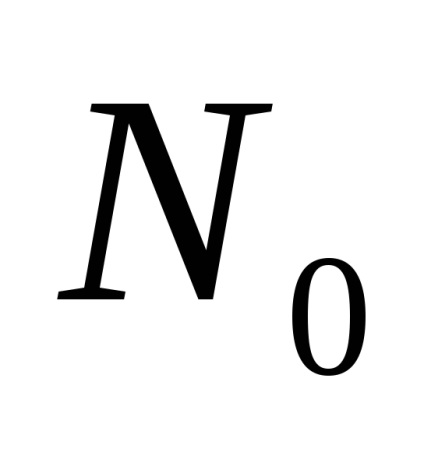Măsurarea tensiunii din hală ca funcție a curentului cu un câmp magnetic constant: determinarea densității și a mobilității purtătorilor de sarcină.
Măsurarea tensiunii Hall în funcție de câmpul magnetic la un curent constant: determinarea coeficientului Hall.
Măsurarea tensiunii în funcție de temperatură.
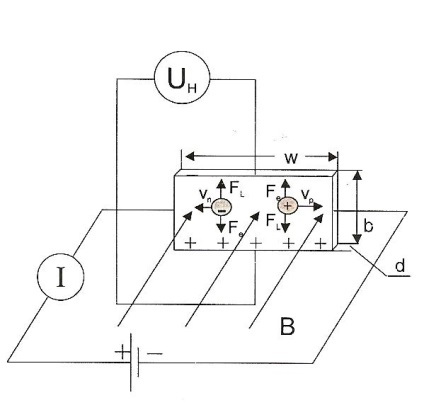
Efectul Hall este o metodă experimentală importantă care face posibilă determinarea parametrilor microscopici ai particulelor în metale și semiconductori.
Pentru a monitoriza efectul Hall în acest experiment utilizând un eșantion de tip n germaniu sub forma unui dreptunghi, plasat într-un poleB magnetic uniform așa cum este prezentat în Fig.1. Dacă curentul trece prin eșantion, tensiunea electrică (tensiunea Hall) este setată perpendicular pe câmpul magnetic. Astfel, curentul este cauza efectului Hall, care în acest caz este descris:
R este coeficientul Hall, care depinde de material și de temperatură. În condiții de echilibru (figura 1), pentru câmpurile magnetice slabe coeficientul Hall
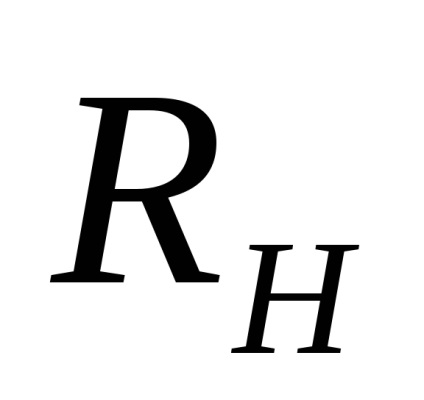
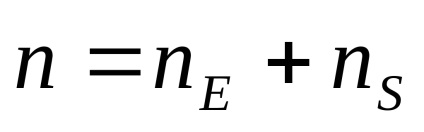
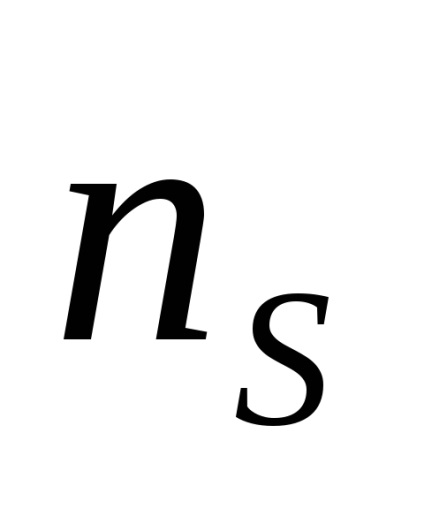
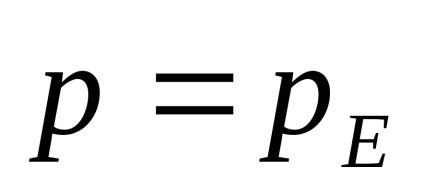
Rezultă din ecuația (2): polaritatea purtătorilor de sarcină predominanți poate fi determinată de la
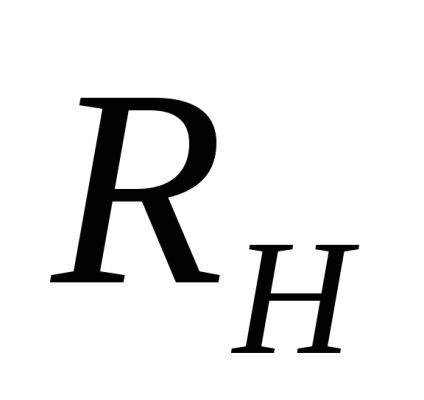
Elementele impurității, grupa 5, cum ar fi antimoniu, fosfor, cum, Ge în rețeaua cristalină a crea electroni suplimentare în banda de conducție (figura 2).
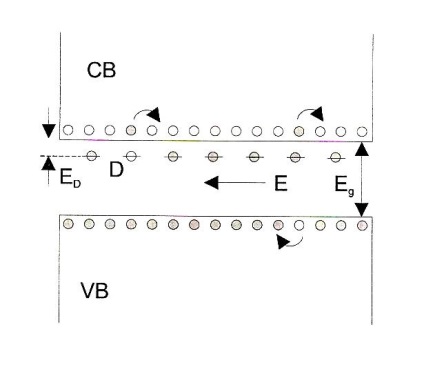
Lor E energie de activare, aproximativ egală cu 0,01 eV, semnificativ mai mică decât energia E de activare (zona intermediară, zona de blocare) electroni miez și găurile de mișcarea termică (caracteristică purtătorilor de sarcină). La temperatura camerei în germaniu dopat, densitatea electronului predomină peste densitatea purtătorilor de sarcină intrinsecă (
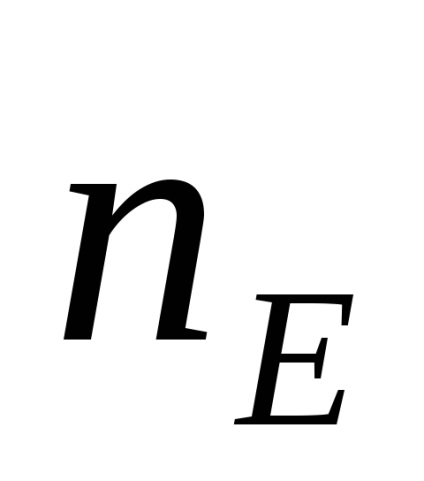
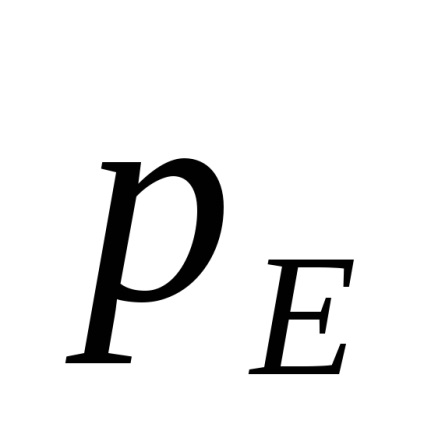
Din ecuațiile (1) și (2) rezultă că:
Mobilitatea este o măsură a interacțiunii dintre suporturile de încărcare și zăbrelele de cristal. Se determină mobilitatea (în cazul germaniului de tip n, a mobilității
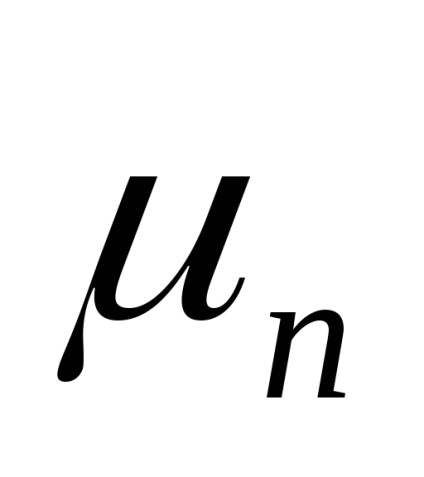
Câmp electric electric datorită căderii de tensiune
Câmpul electric E poate fi determinat prin reducerea tensiunii U și a lungimii probei de germaniu:
Rata de drift poate fi determinată de starea de echilibru în care forța Lorentz este compensată de energia electrică care apar datorită câmpului Hall (Fig.1)
unde puteți folosi dependența
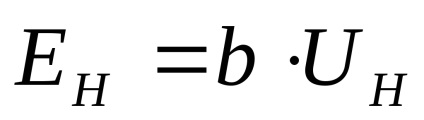
Substituirea ecuațiilor (5) și (7) în ecuația (4), mobilitatea găurilor poate fi calculată la temperatura camerei ca raport:
Curentul I într-un semiconductor este creat atât de un flux de găuri, cât și de electroni:
Densitatea purtătorului depinde de concentrația și temperatura impurităților. La o temperatură scăzută, legăturile se rup, electronii sunt eliberați. Densitatea electronilor impurităților
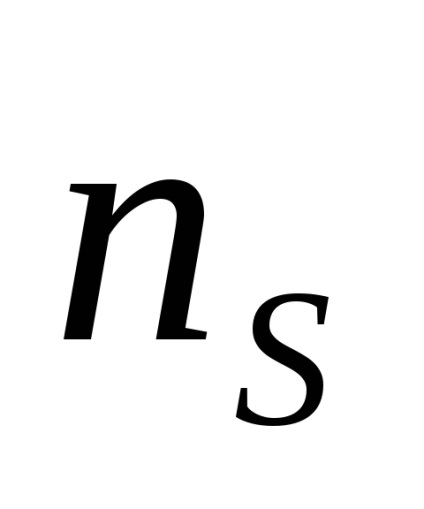
Dependența tensiunii Hall pe temperatură se bazează pe ecuațiile simple (1) și (2):
Să presupunem că mobilitatea electronilor și a găurilor este diferită. Introducem factorul de mobilitate
Apoi ecuația (2) poate fi rescrisă:
Pentru semiconductoarele pure, dependența numărului de suporturi de încărcare de temperatura poate fi reprezentată ca
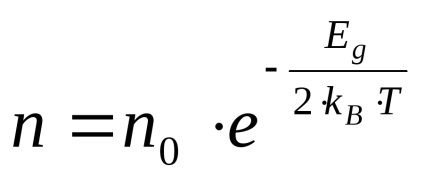
J / K este constanta Boltzmann.
Produsul densităților este dependența de temperatură:
unde densitatea
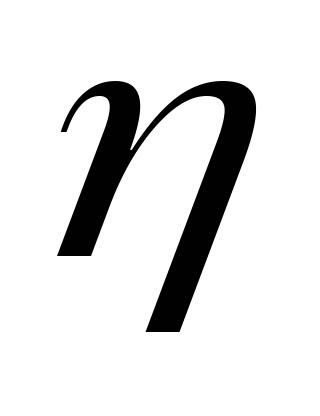
densitate
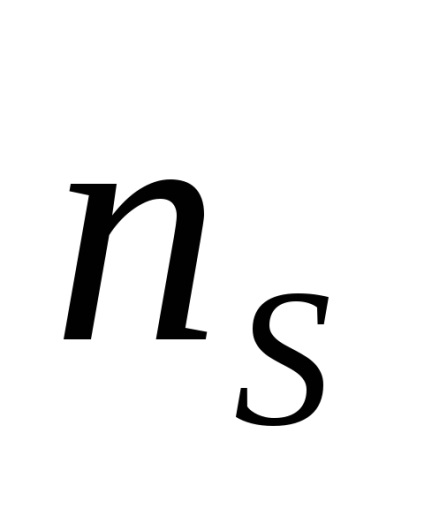
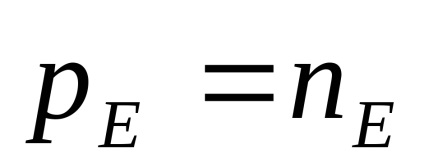
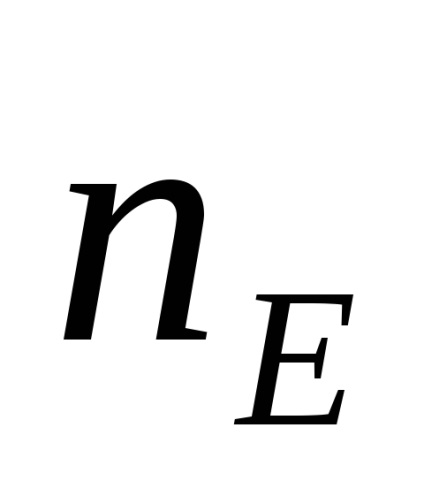
Utilizând ecuațiile (11), (15),