Vom folosi Mathcad pentru a aproxima punctele date folosind funcțiile de putere și liniare. Definiți suma abaterilor pătrat pentru punctele nodale (Figura 13):
Pentru o funcție de alimentare, această cantitate este de 43.684.
Pentru o funcție liniară, această valoare este 740,782.
Se poate concluziona că cu ajutorul funcției de putere obținem o aproximare mai precisă.

Figura 13. Aproximarea punctelor în Mathcad
Construim grafice de aproximare a funcțiilor pe un plan de coordonate (figura 14).
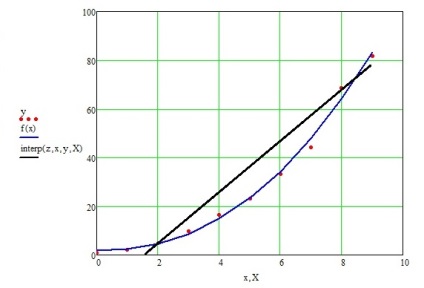
Fig.14 Grafice de aproximare a funcțiilor
Vom aproxima punctele folosind Excel. Pentru a face acest lucru, mai întâi completați tabelul inițial de puncte și notați aceste puncte pe grafic (figura 15).
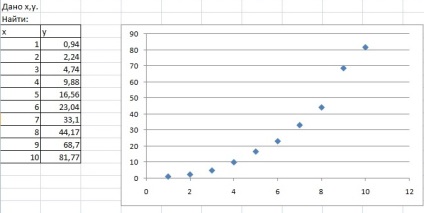
Fig. 15. Puncte de referință pentru aproximarea graficului
Apelați meniul contextual pentru unul dintre punctele de pe diagramă și selectați elementul "Adăugați o linie de tendință ...". În primul rând, o aproximăm cu ajutorul unei funcții de alimentare. Pentru aceasta, selectați "Power" în caseta de dialog "Trend Line" care se deschide.
În mod similar, adăugați o linie de tendință bazată pe o funcție liniară. În setările liniilor de trend, puneți o bifă "arată ecuația pe diagramă". Rezultatul este arătat în Fig. Următoarele funcții aproximative au fost obținute:
Pentru o funcție de alimentare:
y = 0,672x 2,014 +2,072
Pentru o funcție liniară:
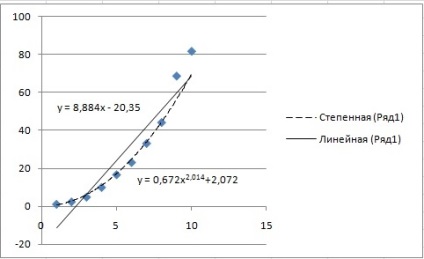
Figura 16. Obținerea graficelor funcțiilor de aproximare
Definiți suma deviațiilor pătrat pentru funcțiile obținute la punctele nodale (Figura 17). Avem:
Pentru o funcție de alimentare, această cantitate este 178.4447864.
Pentru o funcție liniară, această valoare este 740.78208.
În consecință, aproximarea setului de date al funcției de putere este mai precisă decât funcția liniară.
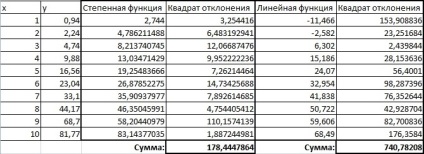
Figura 17. Calcularea în Excel a sumei abaterilor pătrat pentru aproximarea funcțiilor
Când efectuăm aproximația în Mathcad și Excel, am obținut că Mathcad ne permite să construim o funcție de aproximare a puterii cu abilitatea de a specifica o ecuație a unei legi de putere aproximând funcția cu un coeficient liber, care nu poate fi efectuat în Excel. Acest lucru indică deficiențe în Excel atunci când efectuați sarcini similare.
Găsiți extrema unei funcții a două variabile:
în Excel și Mathcad. Construiți un grafic de suprafață bidimensional în Excel și Mathcad.
Să construim un grafic al unei suprafețe bidimensionale în Mathcad (Figura 18)
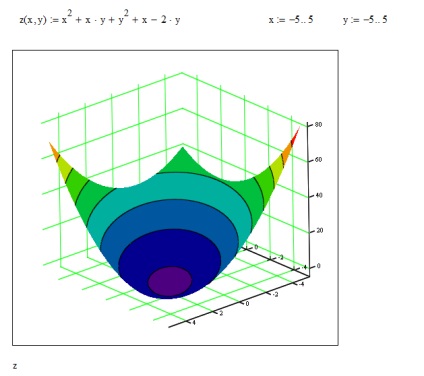
Figura 18. Construcția de suprafețe în Mathcad
Conform graficului, determinăm că funcția z are un singur extremum, un punct minim. Folosim funcția Minimize pentru aproximarea inițială a punctului minim pe care o luăm; . Ca limitare, indicăm intervalele pentru u. Am o soluție. (Figura 19)
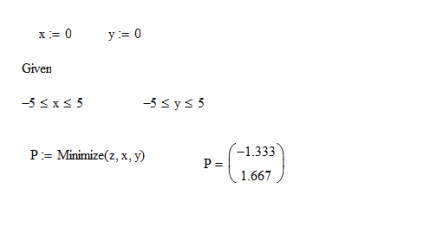
Fig.19 Găsirea valorilor minime folosind Mathcad
Pentru a face acest lucru, vom tabula mai întâi funcția în pași de 1 pe interval cu u (Figura 20).
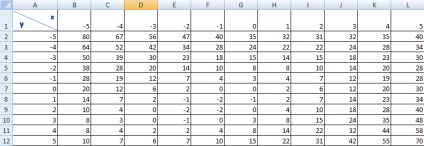
Fig.20.Tabularea funcției a două variabile în Excel
Pe baza tabelului rezultat, construim o suprafață (Figura 21).
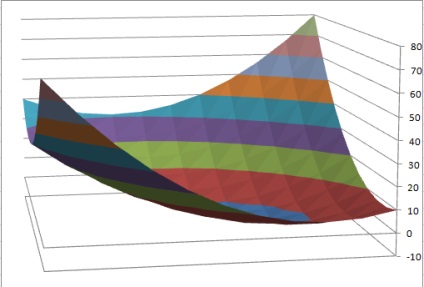
Figura 21. Funcția grafică a 2 variabile în Excel
Excel și Mathcad vă permit să rezolvați rațional problemele de inginerie puse la dispoziția utilizatorului. Ca urmare a muncii depuse, putem trage o concluzie cu privire la superioritatea lui Mathcad față de Excel în rezolvarea problemelor matematice prezentate în cursul lucrărilor.
Lucrarea de curs finalizată a permis consolidarea cunoștințelor existente despre Excel și Mathcad și, de asemenea, a permis să învețe mai multe despre capabilitățile acestor pachete software. În plus, pe baza cunoștințelor practice, a devenit posibil să se spună despre meritele și dezavantajele programelor utilizate în rezolvarea problemelor.