Sortați algoritmi. Partea 1
Toate metodele de sortare existente diferă între ele în ceea ce privește viteza de execuție, comprehensibilitatea și lungimea codului, în frumusețea soluției. Adesea, se fac modificări ale codului algoritmului deja dezvoltat și apar atât de multe decizii, dintre care unele vom încerca acum să le luăm în considerare.
Cu toate acestea, trebuie remarcat faptul că studiul algoritmilor nu este o sarcină ușoară, necesită o analiză atentă a fiecărei linii. Desigur, dacă utilizați butoanele Ctrl + C și Ctrl + V, programul dvs. nu se va înrăutăți, dar în opinia mea nimic nu este mai rău atunci când programatorul nu înțelege pe deplin modul în care funcționează programul său.
Sortați după alegere
Și vom începe cu opțiunea de sortare. Deși acest algoritm nu este cel mai rapid, am decis să încep cu acesta deoarece, în opinia mea, este cel mai simplu de înțeles. Esența algoritmului este de a găsi elementul cel mai mic din matricea sursă și apoi de a schimba primul element din listă cu cel găsit. După aceea, păstrați cele mai mici dintre cele rămase și schimbați-le cu cel de-al doilea element. Și așa mai departe, până când întreaga listă este sortată.
Astfel, este necesar N + (N-1) + (N-2) +. +1 sau N * N trece pentru a sorta lista.
Listing 1. Sortați după alegere
Variabilele min și max pot restricționa zona de listă în care va fi efectuată sortarea. Pentru a sorta întreaga matrice, trebuie să scrieți următoarele
Listing 2. Codul Delphi / Pascal
SellectionSort (a, 0, mare (a));
Introduceți sortarea
Acesta este, de asemenea, un algoritm extrem de simplu pentru înțelegere. Ideea este să creați o nouă matrice și apoi să inserați secvențial elemente din vechea matrice în noua matrice, astfel încât matricea creată să fie întotdeauna ordonată.
Listare 3. Introduceți sortarea
Dacă vă uitați atent la implementarea algoritmului, veți observa imediat că sunt necesare mai multe pentru a executa algoritmul. decât N * N trece, deci în aplicații unde viteza de execuție a codului este critică, un astfel de algoritm nu este relevant.
Sortarea cu bule
Cel mai frecvent utilizate pentru sortarea listelor parțial ordonate, deoarece este pentru viteza de execuție, iar maximul poate fi egal cu O (N), unde N numărul de elemente de matrice, și O, în timpul o singură trecere prin bucla. Acest algoritm din lista de surse caută perechi de cifre care nu sunt în ordine și apoi le schimbă în locații. Procesul se repetă până când întreaga listă este sortată. Figura arată un exemplu de sortare prin această metodă.
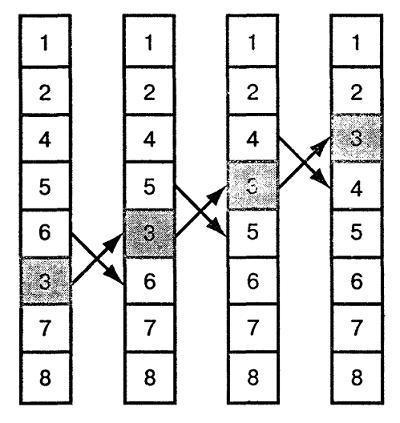
În figură, puteți urmări mișcarea elementului, care a fost inițial mai mică decât după sortare. În timpul ciclului, elementul își schimbă poziția cu o poziție mai apropiată de locația sa finală. În figură, elementul se mișcă spre vârf, ca o bula de aer la suprafața apei. Acest efect a dat și numele algoritmului pentru sortarea bulelor.
Listarea 4. sortarea bulelor
Sortarea rapidă.
Cu acest tip de sortare, matricea este împărțită în două părți, iar apoi se recurge în mod recursiv să le sorteze. Mai mult, elementele primei părți sunt mai mici decât orice element al celei de-a doua părți.
Luați în considerare acest tip de sortare după exemplu:
Dacă algoritmul este numit pentru lista, care conține zero sau un element, abonamentul deja sortate, iar procedura se încheie, în caz contrar un element selectat în raport cu care lista este împărțită în două părți, prima abonament sunt mai puține elemente selectate în a doua mai mult. Apoi, așa cum am menționat deja, se recurge recursiv la sortarea tapetului sub-listelor.
Listarea 5. Sortare rapidă
De asemenea, este de remarcat faptul că o astfel de sortare este cel mai bine utilizată pentru comandarea elementelor de tablă în care urmează absolut, accidental. În timp ce, dacă lista este practic ordonată, ar fi mai înțelept să folosiți sortarea cu bule. În plus, în cazul în care lista este suficient de lungă, algoritmul va provoca recursivitate profundă și, eventual, o depășire a stivei și, ca o consecință, va fi suspendată sau ieșirea de pe urma programului.
Sortați după metoda Shell.
O altă metodă de sortare este sortarea prin metoda Shell. Ideea principală a acestui algoritm este de a crea mai întâi o tulburare de masă în matrice prin compararea elementelor îndepărtate. După cum se poate observa, intervalul dintre elementele comparate scade treptat până la unitate. Aceasta înseamnă că, în etapele ulterioare, sortarea este redusă pur și simplu la permutarea elementelor învecinate (dacă, desigur, sunt necesare astfel de permutări).
Listing 6. Sortați după Shell
Concluzia.
P.S. Comentarii, solicitări și adăugiri la acest articol, vă rugăm să lăsați pe forum.