Căutarea ecuației tangentei la graficul funcției la un anumit punct este cea mai simplă sarcină pentru aplicarea derivatului. Cel mai simplu mod de a obține un răspuns rapid este să folosiți Wolfram | Alpha.
Wolfram | Alpha rezolvă cu adevărat aceste probleme rapid și ușor. Nu trebuie să ne amintim cum arată ecuația generală a tangentei. Nici nu trebuie să calculam valoarea funcției și a derivatului acesteia la un anumit punct, sau să o înlocuim în ecuația generală a tangentei și apoi să simplificăm ecuația rezultantă. Cu Wolfram | Alpha, nu este nevoie de nimic. Este suficient doar să folosiți linia tangentă a solicitării (în limba engleză "tangent line" - tangentă).
De exemplu, ca în Wolfram | Alpha, o astfel de problemă este rezolvată; "Găsiți ecuația tangentei la graficul funcției y = x ^ 2 la punctul x = 1".
- tangentă de x ^ 2 la x = 1
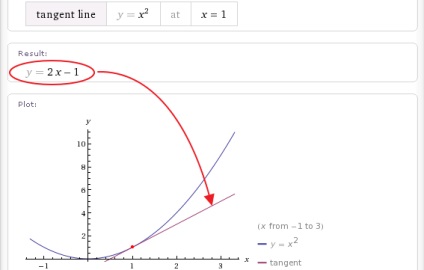
După cum puteți vedea, Wolfram | Alpha afișează nu numai ecuația de tangență, ci și o ilustrare grafică.
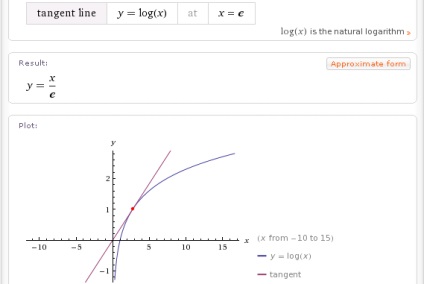
- linia tangentă y = (sinx) ^ 3 la x = 11pi / 12
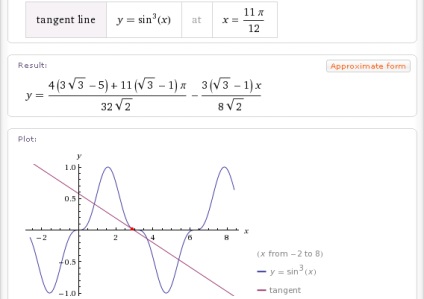
- linia tangentă y = sinx + lnx la x = 3e
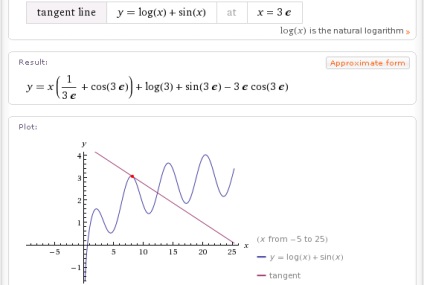
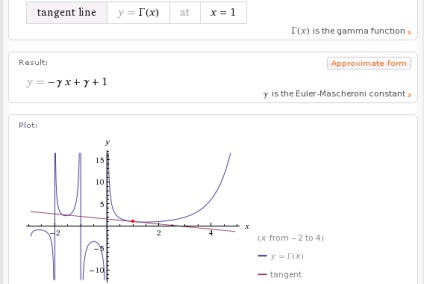
În plus, Wolfram | Alpha poate găsi ecuația de tangente chiar și pentru funcții speciale, de exemplu, cum ar fi funcția gamma: