1. Alegerea formei de deschidere a oglinzii
2. Alegerea funcției de distribuție a amplitudinii câmpului în deschiderea oglinzii
3. Calcularea mărimii deschiderii
4. Calcularea alimentatorului DI
5. Selectarea și proiectarea iradiatorului
6. Proiectarea unui alimentator de corn
7. Calcularea distribuției reale a câmpului și a oglinzii oglinzii
Antenele cu oglindă sunt cele mai comune tipuri de antene direcționale în lungimi de undă centimetru, decimetru și parțial. Răspândită antene utilizare reflector explicat simplitate de construcție, posibilitatea de a obține aproape orice tip utilizat în practica NAM, cu randament ridicat, temperatura de zgomot redus, o bună gamă de proprietăți, etc.
sunt utilizate Principalele tipuri de oglinzi în antene reflector: parabolic (paraboloid trunchiat paraboloid de rotație, un cilindru parabolic), sferice, plate și înclinate cu două, cu formă specială și multimirrors.
În aplicațiile radar, antene fel de mâncare face mai ușor pentru a primi regiunea equisignal, permite formarea simultană a mai multor Nam oglindă comune (inclusiv suma și diferența). Unele tipuri de antene cu oglindă pot oferi un fascicul suficient de mătuitor într-un sector unghiular semnificativ. Antenele reflector sunt cel mai frecvent tip de antenă în domeniul comunicațiilor spațiale și astronomie, și anume printr-antene reflectoare capabile să creeze structuri de antenă gigant cu o deschidere efectivă a suprafeței, măsurată în mii de metri pătrați.
1. Alegerea formei de deschidere a oglinzii
Secvența de calcul a părții radiante a antenei oglinzii (AP) depinde de natura atribuire tehnică (TOR) pentru proiectare.
De regulă, alocarea țintă a antenei, frecvența de operare și cerințele pentru proprietățile direcționate ale antenei, care trebuie analizate, sunt specificate în TOR.
reprezentanți clasici antene reflector sunt antene parabolice care pot fi realizate sub forma unui paraboloid de revoluție sau un cilindru cu structură închisă parabolic delimitată de planuri conductoare paralele.
Pentru a selecta forma de deschidere a antenei, este necesar să se analizeze raportul lățimii NW în planurile E și H. Pentru versiunea mea, acest raport
Prin urmare, forma deschiderii oglinzii este rotundă. Acest lucru poate fi un paraboloid de revoluție, este iluminator omnidirecțională excitat (de exemplu, piesa bucală), plasat în focarul oglinzii, și convertește frontul de undă sferice într-un plan.
Principiul de funcționare al antenei parabolice este următoarea: constă dintr-un reflector metalic (reflector) 1, iluminatorului 2, plasat în centrul unui paraboloid de revoluție, și alimentator de alimentare cu 3 (figura 1.).

Iradierea antenei este proiectată astfel încât aproape toată energia emisă de ea să fie îndreptată către reflector. Undele electromagnetice excită curenții de înaltă frecvență pe suprafața lor, care creează propriile lor câmpuri electromagnetice. Deoarece suprafața reflectorizantă este atașat la o formă parabolică, suma distanțelor de focalizarea la reflector și de reflector într-un plan perpendicular pe axa focală, este constantă, astfel încât suprafața deschiderii antenei reemitted oscilații vin la aceeași fază.
Ca urmare a adăugării oscilațiilor reflectate, se formează o undă plană în deschiderea antenei și apoi se extinde de-a lungul axei sale.
Indicăm principalii parametri geometrici ai oglinzilor parabolice:
R, f - raza și lungimea focală a oglinzii; y0 este unghiul deschiderii oglinzii;
p (Y) este profilul oglinzii; coordonata x a punctului din deschiderea oglinzii. Acești parametri sunt legați de relații simple:
2. Alegerea funcției de distribuție a amplitudinii câmpului în deschiderea oglinzii
Alegem funcția de distribuție a amplitudinii în funcție de condiția dată din tabele.
Grafice ale distribuțiilor corespunzătoare:
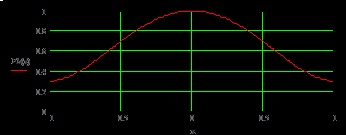
Fig. 2 Distribuția câmpului în planul H al deschiderii.
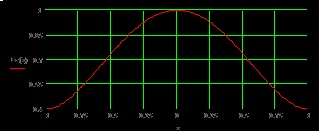
Fig. 3 Distribuția câmpului în planul E al deschiderii.
3. Calcularea mărimii deschiderii
Dimensiunile deschiderii depind de lățimea DN, de lungimea de undă de lucru și de funcțiile de distribuție selectate.
în două planuri:
Lățimea NW în două planuri de la TK:
Să găsim lungimea de undă:
Alegem raza de la o dimensiune mai mare: R = b / 2, R = 35 cm.
Pentru a asigura o anumită lățime a modelului de radiație, luăm ca deschidere un paraboloid trunchiat simetric de revoluție.
4. Calcularea alimentatorului DI
În paraboloidul revoluției (sau un paraboloid trunchiat de revoluție), iradiatorul trebuie să creeze un val sferic. Într-un astfel de val, amplitudinea scade odată cu creșterea distanței r de la sursă (iluminator) invers proporțională cu r (într-un mediu fără pierderi). După reflectarea din oglindă, frontul valurilor devine plat, iar amplitudinea unei valuri plane într-un mediu fără pierderi nu depinde de distanța.
Plecând de la cele de mai sus, relația dintre dioda iradiatorului f (y) și câmpul din deschidere, până la un factor constant, poate fi scrisă sub forma:
,
.
Normalizarea Nam fmax maximă (y) = r (0) E (0) = f, obținem o formulă de calcul pentru iradiatorul Nam normalizat:
.
Din fig. 1 se poate vedea acest lucru
,
.
Se observă că coordonata normalizată x ar trebui găsită prin următoarea formulă:
.
Valoarea lui y0 este aleasă aproximativ în intervalul 58 ° - 62 °. Acest lucru face posibilă asigurarea în viitor a unui QIB suficient de mare, cu o dimensiune relativ mică a iradiatorului și, prin urmare, cu o mai mică umbrire a oglinzii. Cu scăderea y0, DI necesar al iradiatorului poate fi atât de larg încât dimensiunile iradiatorului să devină mai mici decât, de exemplu, chiar și la capătul deschis al ghidului de undă. Am setat unghiul de deschidere în planul E:
.
iar dimensiunea deschiderii ne permite să găsim lungimea focală a oglinzii cu formula:
Deoarece lungimea focală a unui paraboloid de revoluție (sau un paraboloid trunchiat) într-un alt plan trebuie să fie același, unghiul deschiderii într-un alt plan
este determinată automat de f și de dimensiunea b în acest plan. Din moment ce
,
.
Mai mult, calculăm alimentatorul DN în planurile E și H, respectiv:
,
,
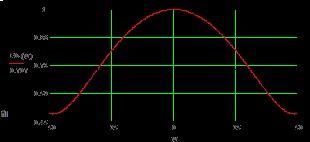
Fig. 4. LT a iradiatorului din planul E.
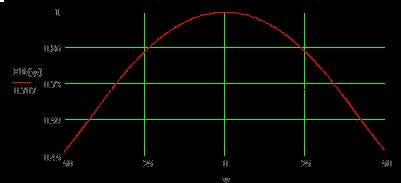
Fig. 5. DN al iradiatorului în planul H.
Din fig. 4 și Fig. 5 este ușor de determinat lățimea DN a alimentatorului în planurile principale:
.
5. Selectarea și proiectarea iradiatorului
Pentru iradiere, de regulă, se îndeplinesc următoarele cerințe:
a) trebuie să realizeze modelul de radiație calculat anterior în sectorul unghiurilor
și au radiații minime în afara acestui sector;
b) dimensiunile sale transversale trebuie să fie minime pentru a reduce umbrirea deschiderii;
c) iradiatorul trebuie să aibă un centru stabil de fază comună în două planuri, compatibil cu focalizarea paraboloidului de revoluție;
d) rezistența electrică a iluminatorului trebuie să fie suficientă pentru a transmite puterea totală de lucru a emițătorului în impuls, fără pericolul de defecțiune;
e) banda de frecvență de lucru a iradiatorului trebuie să corespundă benzii de frecvență a antenei;
e) proiectarea iradiatorului ar trebui să asigure rezistența necesară la condițiile meteorologice și să permită posibilitatea de etanșare a întregii căi de alimentare;
Ca un iradiator luăm un corn piramidal (figura 6).
6. Proiectarea unui alimentator de corn

Fig. 6. Cornul piramidal.
Calcularea antenei cornului se reduce la calcularea dimensiunilor sale geometrice. Dimensiunile deschiderii
alegem pe baza surselor de iradiere găsite anterior în două planuri.
Dimensiunile ajustate ale difuzorului:
ghidul de undă bazat pe următoarele considerente: ghidul de undă trebuie să se asigure că trece numai valul principal de tip și să treacă puterea necesară. Pentru acest scop este potrivit un ghid de undă standard de 23x10 mm. Din tabel. 3. [1] constatăm că acest waveguide admite
kW, care este mai mare decât puterea necesară. Din aceeași masă, alegeți materialul cu cea mai mică pierdere - cupru (
Să determinăm lungimea cornului optim
, determină lungimea cornului în planul E din starea de andocare a claxonului cu ghidul de undă:
consultați Pentru a vă asigura că cornul este optim, este necesar să faceți această condiție
cm, adică Condiția de optimitate în planul E este de asemenea satisfăcută,
Calculăm erorile de fază:
,
Calculăm diagrama actuală de directivitate a difuzorului.
- modulul coeficientului de reflexie al valului de la deschiderea claxonului;
;
.
.
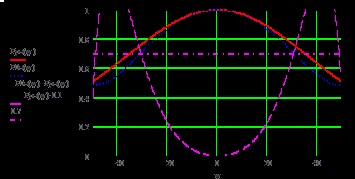
Fig. 7. ND real și necesar al iradiatorului în planul E.
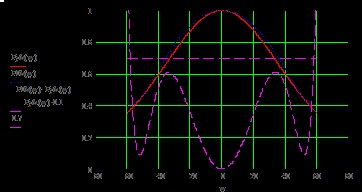
Fig. 8. ND real și necesar al iradiatorului din planul H
Se calculează pozițiile centrelor de fază a cornului în planurile principale:
,
Toleranța pentru deplasarea centrului de fază al iluminatorului de la focalizare de-a lungul axei:
între centrele de fază satisface toleranța pentru deplasarea centrului de fază al iradiatorului de la focalizarea oglinzii de-a lungul axei sale.
7. Calcularea distribuției reale a câmpului și a oglinzii oglinzii
Calculul este efectuat pentru a compara realitatea
distribuțiile în deschiderea oglinzii. În paraboloidul trunchiat de rotație, NW real este legat de ND normalizat al iradiatorului prin următoarea relație:
,
.
Graficele distribuției reale și ideale și erorile lor relative sunt reprezentate pe același grafic. Eroarea nu trebuie să depășească 7%.
Având în vedere toate cele de mai sus, vom calcula distribuția reală a câmpului în oglindă:
1) Calculul distribuției reală a amplitudinii câmpului în planul E
Funcția reală de distribuție are forma:
.
.
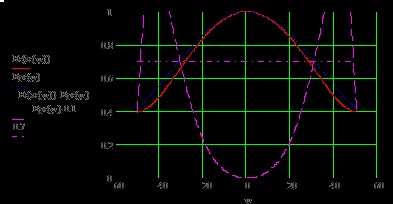
Fig.9 Graficul distribuției reale a câmpului în planul E
2) Calculul distribuției reale a amplitudinii câmpului în planul H.
Funcția reală de distribuție are forma:
.
.
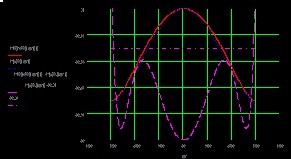
Fig. 10. Distribuția reală și ideală a câmpului în planul H și eroarea lor relativă.
Calculul NAM se bazează pe formulele date în [1]. Aceste formule sunt date fără a lua în considerare DN-ul elementului Huygens, deci le multiplicăm
:
;
.
Vom compune diagrama de directivitate la o scară logaritmică. Pentru aceasta transformăm forma
.
În mod similar pentru planul E:
;
;
sau la o scară logaritmică
.
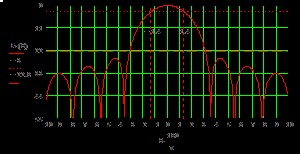
Fig. 11. DS a antenei oglinzii în planul E
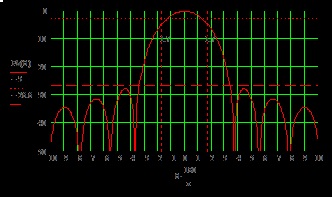
Fig. 12. DS a antenei oglinzii în planul H