Parabola (Figura 4.16)
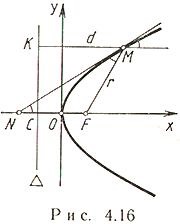
Să presupunem că planul definit la punctul F și linia nu trece prin F. Parabolă - mulțimea tuturor punctelor M plan, fiecare dintre care este echidistant față de punctele F și drepte. Punctul F se numește focalizare, linia este direcția directă a parabolei; (OF) - axa, O - vârf - parametru - focus - raza focală.
Ecuația tangentei la un punct
Proprietatea tangentei la parabolei: (M - punctul tangență; N - punctul de intersecție al tangentei cu axa Ox).
Ecuația normală într-un punct
Ecuația diametrului conjugat la coarde cu coeficientul unghiular k. y = p / k.
Ecuațiile parametrice ale unei parabole:
Parabolă, ecuația canonică a parabolei, excentricitatea parabolei, ecuațiile parametrice ale parabolei, ecuația polară a parabolei, proprietatea tangenta la parabolei.