Diviziunea numerelor negative Cum se efectuează divizarea numerelor negative - numărul paginii 1/1
Diviziunea numerelor negative
Cum se efectuează împărțirea numerelor negative este ușor de înțeles, amintindu-ne că diviziunea este o acțiune opusă multiplicării.
Dacă a și b sunt numere pozitive, atunci împărțirea a cu un număr b înseamnă găsirea unui număr c care, înmulțit cu b, dă numărul a.
Această definiție a diviziunii acționează pentru orice număr rațional dacă divizorii nu sunt zero.
Prin urmare, de exemplu, pentru a împărți numărul (-15) cu numărul 5 - înseamnă a găsi un număr care, înmulțit cu numărul 5, dă numărul (-15). Un astfel de număr va fi (-3), deoarece
Exemple de împărțire a numerelor raționale.
10. 5 = 2, deoarece 2 • 5 = 10
(- 4). (-2) = 2, deoarece 2 • (- 2) = - 4
(- 18). 3 = - 6, deoarece (- 6) • 3 = - 18
12. (- 4) = - 3, deoarece (- 3) • (- 4) = 12
Se poate observa din exemple că numărul doi numere cu aceleași semne este un număr pozitiv (exemplele 1, 2), iar coeficientul a două numere cu semne diferite este un număr negativ (exemplele 3, 4).
Reguli pentru divizarea numerelor negative
Pentru a găsi modulul coeficientului, trebuie să împărțiți modulul divizibil într-un modul divizor.
Deci, pentru a împărți cele două numere cu aceleași semne. aveți nevoie de:
modulul divizibil este împărțit într-un modul divizor;
înainte de a pune semnul "+".
Exemple de numere împărțite cu aceleași semne:
(- 9). (- 3) = + 3
6. 3 = 2
Pentru a diviza două numere cu semne diferite. aveți nevoie de:
modulul divizibil este împărțit într-un modul divizor;
înainte de rezultat puneți semnul "-".
Exemple de numere împărțite cu semne diferite:
(- 5). 2 = - 2,5
28. (- 2) = - 14
Pentru a determina semnul privat, puteți utiliza și tabelul următor.
Regula despre semne în diviziune
Când se calculează expresii "lungi", în care sunt implicate numai înmulțiri și împărțiri, este foarte convenabil să se folosească regula semnelor. De exemplu, pentru a calcula fracțiile
Puteți avea grijă ca numitorul să aibă 2 semne minus, care, înmulțite, vor da un "plus". De asemenea, în numitor sunt trei semne minus, care, înmulțite, vor da "minus". Prin urmare, la final, rezultatul va fi un semn minus.
Reducerea fracțiunii (acțiuni ulterioare cu modulele de număr) se realizează ca mai înainte:
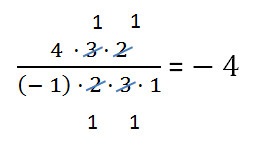
Coeficientul unei divizări de zero cu un număr diferit de zero este zero.
Împărțiți cu zero NU POATE!
Toate regulile anterioare de divizare printr-un act asupra setului de numere raționale.
a. 1 = a
a. (-1) = -a
a. a = 1
, unde a este un număr rațional.
Dependențele dintre rezultatele de multiplicare și divizare, cunoscute pentru numere pozitive, sunt, de asemenea, păstrate pentru toate numerele raționale (cu excepția numărului zero):
dacă a • b = c; a = c. b; b = c. o;
dacă a. b = c; a = c • b; b = c. o
Aceste dependențe sunt folosite pentru a găsi un multiplicator necunoscut, divizibil și divizor (atunci când se rezolvă ecuațiile) și, de asemenea, pentru a verifica rezultatele multiplicării și divizării.
Un exemplu de găsire a unui necunoscut.
x = - 2
Semnul minus în fracții
Împărțim numărul (-5) cu 6 și numărul 5 cu (-6).
Vă reamintim că linia din înregistrarea fracțiunii obișnuite este același semn de împărțire și se notează coeficientul fiecăreia dintre aceste acțiuni sub forma unei fracții negative.
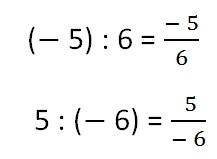
Astfel, semnul minus din fracțiune poate fi:
înainte de împușcare;
în numărător;
în numitor.
Când scrieți fracții negative, semnul minus poate fi plasat înaintea fracțiunii, transferați-l de la numitor la numitor sau de la numitor la numărător.
Acest lucru este adesea folosit atunci când efectuați acțiuni cu fracțiuni, făcând calculele mai ușoare.
Un exemplu. Rețineți că, după ce ați luat semnul minus în fața bracket-ului, scădăm cele mai mici prin regulile de adăugare a numerelor cu semne diferite de la modulul mai mare.
Folosind proprietatea descrisă de a purta un semn în fracțiuni, se poate acționa fără a ști care este modulul acestor numere fracționate este mai mare.