Caracteristicile structurii lichidului, vezi în prima parte a cursului 20 Proprietăți ale lichidelor
Caracteristica cea mai interesantă a lichidelor este prezența unei suprafețe libere.
Suprafața unui lichid care nu atinge pereții vasului se numește o suprafață liberă. Se formează ca rezultat al acțiunii gravitației asupra moleculelor lichidului.
Lichidul. spre deosebire de gaze, nu umple întregul volum al vasului în care este umplut. Între lichid și gaz (sau vapori), se formează o limită care se află în condiții speciale în comparație cu restul de masă fluidă. Moleculele din stratul limită al lichidului, spre deosebire de moleculele din adâncime, sunt înconjurate de alte molecule ale aceluiași lichid, nu de toate părțile. Forțele interacțiunii intermoleculare, care acționează asupra uneia dintre moleculele din interiorul lichidului din partea moleculelor învecinate, sunt în medie compensate reciproc. Orice moleculă din stratul de frontieră este atrasă de moleculele localizate în interiorul lichidului (forțele care acționează asupra unei molecule lichide date din partea moleculelor de gaz (sau a vaporilor) pot fi neglijate). Ca rezultat, apare o anumită forță rezultantă, îndreptată spre interiorul lichidului. Dacă molecula se deplasează de la suprafață la interiorul lichidului, forțele interacțiunii intermoleculare vor face o treabă pozitivă.
În schimb, pentru a trage un anumit număr de molecule de la adâncimea lichidului la suprafață (adică pentru a mări suprafața lichidului), este necesar să se exercite activitatea pozitivă a forțelor externe ΔAvnesh. proporțional cu schimbarea ΔS a suprafeței:
Coeficientul σ se numește coeficientul de tensiune superficială (σ> 0) sau pur și simplu tensiunea superficială.
Coeficientul de tensiune superficială este egal cu munca necesară pentru a mări suprafața lichidului la o temperatură constantă cu una.
În SI, coeficientul tensiunii de suprafață este măsurat în jouli pe metru pătrat (J / m 2) sau în newtoni pe metru (1 N / m = 1 J / m 2).
În consecință, moleculele stratului de suprafață al lichidului au o energie potențială excesivă în comparație cu moleculele din interiorul lichidului.
Energia potențială Ep a suprafeței lichidului este proporțională cu aria sa: Ep = Awesh = σS.
Se cunoaște din mecanică că stările de echilibru ale sistemului corespund valorii minime a energiei sale potențiale. Ie fiecare sistem intră spontan într-o stare în care potențiala sa energie este minimă. Aceasta înseamnă că lichidul trebuie să treacă spontan într-o stare în care suprafața liberă are cea mai mică valoare. Rezultă că suprafața liberă a lichidului tinde să-și reducă suprafața. Deoarece pentru același volum suprafața cea mai mică a sferei este, lichidul în stare de greutate are forma unei sfere.

Din acest motiv, o picătură liberă de lichid presupune o formă sferică. Fluidul se comportă ca și când forțele tangente la suprafața sa acționează pentru a tăia (contracta) această suprafață. Aceste forțe sunt numite forțe de tensiune superficială.
Forțele care acționează în plan orizontal și contractează suprafața unui lichid se numesc forțe de tensiune superficială.
Prezența forțelor de tensiune de suprafață face ca suprafața filmului întins elastic lichid cum ar fi, cu singura diferență că forța elastică din film depinde de suprafața sa (adică din filmul este deformat), iar tensiunea de suprafață nu depinde de aria suprafeței lichidului.
Unele lichide, cum ar fi apa cu săpun, au capacitatea de a forma filme subțiri. Toate bulele bine cunoscute de săpun au o formă sferică obișnuită - acesta este și efectul forțelor de tensionare de suprafață.
Dacă un cadru de sârmă este plasat în soluția de săpun, o parte a cărei parte este mobilă, atunci acesta va fi acoperit cu un film de lichid.
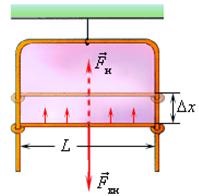
Partea mobilă a cadrului de sârmă este în echilibru sub acțiunea unei forțe exterioare și a forțelor de tensionare de suprafață rezultate. Forțele de tensionare a suprafeței tind să reducă suprafața filmului, astfel că pelicula de săpun va ridica cadrul mobil în sus cu Δx. Pentru a echilibra partea mobilă a cadrului, trebuie aplicată o forță exterioară.
Daca te deplasezi prin forta bara transversala la Δx, atunci munca se va face
unde ΔS = 2LΔx este schimbarea în suprafața ambelor laturi ale filmului de săpun (L este lățimea cadrului).
Deoarece modulele de forță sunt aceleași, putem scrie Fk Δx = σ2LΔx sau σ = Fk / 2L
Coeficientul de tensiune superficială σ este numeric egal cu forța tensiunii de suprafață care acționează pe unitatea de lungime a liniei care leagă suprafața.
Surface natyazhenieeto cantitate fizică egală cu raportul dintre suprafața natyazheniyaF forța aplicată pe suprafața de delimitare a stratului de lichid și tangențial la suprafață la dlineLetoy limită.
Coeficientul de tensiune superficială σ depinde
- din tipul de fluid;
- din prezența impurităților;
- din temperatura.
Forțele de tensionare a suprafeței determină forma și proprietățile picăturilor de lichid, bulele de săpun. Aceste forțe mențin acul din oțel și contorul de apă pentru insecte pe suprafața apei, mențin umiditatea pe suprafața țesutului.
Cu cât tensiunea superficială este mai mică, cu atât mai ușor penetrează lichidul în țesut (la apă - 72,8 mN / m, în soluția de săpun - 25 mN / m).
Lângă limita dintre lichid, solid și gaz, forma suprafeței libere a lichidului depinde de forțele de interacțiune ale moleculelor lichide cu moleculele solidului (interacțiunea cu moleculele gazului (sau vaporii) poate fi neglijată).
În cazul în care picături de apă sunt plasate pe suprafața unui pahar curat, se vor răspândi, iar dacă pe o suprafață grasă, vor lua o formă aproape de forma mingii.
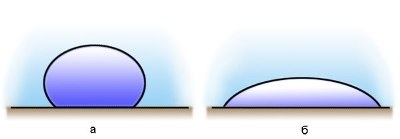
Dacă forțele de interacțiune dintre moleculele unui lichid și moleculele unui solid sunt mai mari decât forțele de interacțiune dintre moleculele lichidului însuși, lichidul va umezi suprafața solidului. (cazul cu picături de apă pe sticlă)
În acest caz, lichidul se apropie de suprafața solidă la un anumit unghi ascuțit, care este caracteristic unei perechi lichide-solide date. Unghiul θ este numit unghiul limită.
Unghiul limită este unghiul dintre suprafața solidului și tangenta la suprafața lichidului în punctul de contact.
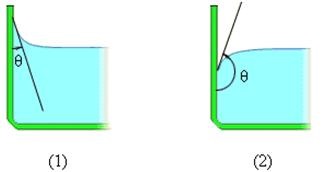
Unghiuri umede de umectare (1) și non-umectare (2) lichide.
Dacă forțele de interacțiune dintre moleculele lichidului depășesc forțele interacțiunii lor cu moleculele solidului, lichidul nu umezește suprafața solidului. (un caz cu picături de apă pe o suprafață grasă, mercur pe sticlă)
În acest caz, unghiul de contact θ se dovedește a fi neclar (Figura 1).
Când se umezește θ <0 (острый), при несмачивании θ> 0 (proastă). Cu umectare completă, θ = 0. pentru o umplere completă, θ = 180 °.
Suprafața curbată a lichidului în tuburile cilindrice înguste sau în apropierea pereților vasului se numește Neman.
Se ridică suprafața lichidului de umectare din apropierea solidului, iar meniscul este concav. În lichidul nonwetting, suprafața sa aproape de corpul solid scade oarecum, iar meniscul este convex.
curbura meniscului lichid este deosebit de bine observate in tuburi subtiri, numite capilare.
Dacă un capilar este coborât într-un vas cu un lichid, lichidul din acesta se va ridica sau va cădea la o anumită înălțime h.
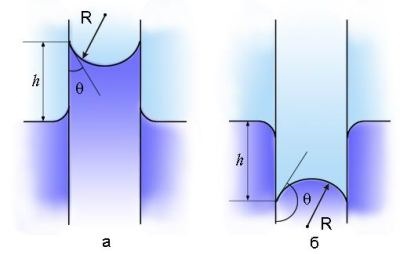
Deoarece suprafața meniscului este mai mare decât suprafața secțiunii interioare a tubului, sub influența forțelor moleculare, suprafața curbată a lichidului tinde să se îndrepte și astfel creează o presiune suplimentară p. care atunci când este udat (meniscul concav) este îndreptat din lichid și când nu este umezit (meniscul convex) - în interiorul lichidului. Mărimea acestei presiuni a fost determinată de fizicianul francez Laplace și, prin urmare, el este numit presiune laplaciană.
Presiunea Laplace este presiunea suplimentară care este creată de suprafața curbă a lichidului.
Când este umed (meniscus concav), este îndreptată din lichid și când nu este umezită (meniscul convex) - în interiorul lichidului.
Pentru o formă sferică a unei suprafețe libere a unui lichid cu raza R, presiunea Laplacian este exprimată prin formula pL = 2σ / R
Fenomenele capilare sunt creșterea sau scăderea lichidului în tuburi cu diametru mic - capilare.
Umezirea lichidelor creste pe capilare, fara umezire - picatura.
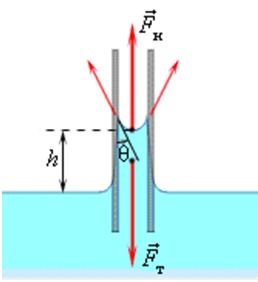
Ridicarea lichidului de umectare în capilar.
Figura prezintă un tub capilar cu o anumită rază r. coborât de capătul inferior într-un lichid umed de densitate ρ.
Capătul superior al capilarului este deschis. Creșterea în fluid capilar continuă atâta timp cât forța gravitațională care acționează asupra fm coloana de lichid din tubul capilar, devine egală cu modulo FH forțe de tensiune de suprafață rezultată care acționează de-a lungul suprafeței de contact de delimitare a lichidului capilar: = fm subsol nr. unde forța gravitațională este Fm = mg. masa m = ρV = ρh πr 2. Atunci Fm = ρh πr 2 g. și astfel forța de tensiune FH = σlcosθ = σ2πrcosθ (l = 2πr)
Cu udarea completă, θ = 0, cos θ = 1. În acest caz, h> 0.
La o răcire completă, θ = 180 °, cos θ = -1 și, în consecință, h <0.
Nivelul lichidului non-umectant din capilară scade sub nivelul lichidului din vasul în care capilarea este coborâtă.
Apa aproape umezește complet suprafața curată a sticlei. Dimpotrivă, mercurul nu umezește complet suprafața de sticlă. Prin urmare, nivelul de mercur din capilarul de sticlă scade sub nivelul din vas. Iar nivelul apei din capilarul de sticlă se ridică.
Fenomenele capilare joacă un rol important în natură și tehnologie. Multe capilare fine se găsesc în plante. În copaci, prin capilare, umiditatea din sol se ridică la vârful copacului, unde prin frunze se evaporă în atmosferă. În sol există capilare, care sunt mai înguste, cu cât solul este mai dens. Apa pe aceste capilare se ridică la suprafață și se evaporă repede, iar pământul se usucă. Aratul timpuriu al pământului distruge capilarele, adică conservă umiditatea solului și crește randamentul.
Procesul de circulație este asociat cu capilaritatea. Vasele sanguine sunt capilare.
În tehnică, fenomenele capilare sunt de mare importanță, de exemplu, în procesele de uscare a corpurilor capilare-poroase etc. Fenomenele capilare sunt de mare importanță în industria construcțiilor. De exemplu, pentru a face un zid de cărămidă nu umed, se face o fundație între fundația casei și perete dintr-o substanță în care nu există capilare. În industria hârtiei este necesar să se ia în considerare capilaritatea în producția de diferite tipuri de hârtie. De exemplu, în producția de hârtie de scris, este impregnat cu un compus special care înfundă capilarele. În viața de zi cu zi, fenomenele capilare sunt folosite în fitiși, în hârtie blotantă, în pixuri de cerneală și altele asemenea.