REZERVAREA REPREZENTĂRILOR NUMERELOR DE DESCĂRCARE A MULTICHIMĂRILOR PE STRUCTURI DE DATE MODULARE
1 Instituția de învățământ superior de învățământ superior "Universitatea de Stat din Surgut"
Lucrarea descrie paralelizarea reprezentărilor numerelor de superimprimare din mai multe cifre utilizând sistemul de clasă reziduală (COK), teorema reziduală chineză (CTO) și teorema Minor Fermat. Această reprezentare a numerelor de mai multe cifre oferă avantaje în timp pentru operațiile de calcul cu o cantitate semnificativă de date prelucrate, deoarece toată prelucrarea informațiilor trece în paralel și independent unul de celălalt. O reprezentare paralelă poate afișa un milion sau mai multe numere de biți și poate fi utilizată pe scară largă atât în codarea informației, în algoritmi ultra-rapizi, cât și în testarea supercomputerelor. În ciuda unor deficiențe, care la rândul lor pot fi depășite, sistemul modular sau sistemul de clasă reziduală este un mediu matematic unic pentru calculul paralel. Prin urmare, acest sistem poate fi luat în considerare atunci când se dezvoltă sisteme de înaltă performanță bazate pe procesoare logice integrate programabile (FPGA) și multi-core.
Teorema restului chinezesc
Teorema lui Fermat
sistem de clasă reziduală
1. Amerbaev V.M. Bazele teoretice ale aritmeticii computerizate. - Alma-Ata: Science, 1976. - 320 p.
2. Bukhshtat AA Teoria numerelor. - M. Nauka, 1975.
3. Vasilenko ON Metode moderne de verificare a simplității numerelor. // Colectarea cibernetică. O nouă serie. - 1988. - Problema. 25. - pag. 162-187.
În teoria algoritmică modernă, numerele mari și super-mari joacă un rol important în criptografie pentru construirea de cipuri de complexitate variabilă și pentru testarea performanțelor supercomputerelor [4, 8]. Studiul numerelor super-mari [5] a arătat că acestea au cantități care sunt dificil sau aproape imposibil de reprezentat biți pe biți în sistemele convenționale de număr de poziții.
Dacă numărul A = 22147483647 este ridicat la gradul specificat, atunci va avea mai mult de un milion de cifre. Prin urmare, este imposibil să reprezentăm astfel de numere în sistemul de numere pozitive generalizate în starea inițială naturală.
Vom reprezenta numere superimprimate din mai multe cifre folosind sistemul de numere pozitionale obisnuite, sub forma unui sistem informatic, aratat in schema de calculare a numerelor super-mari (Figura 1) si le vom analiza.
Diagrama arată că intrarea numerelor ultralarge algoritmul de calcul (săgeata stânga) vin numere multibit foarte mari, săgeți „de sus în jos“ denota sistem numeric de poziție și operații aritmetice. La ieșirea algoritmului, un rezultat foarte mare este rezultatul. Cu toate acestea, dacă numărul de rezultate este afișat în sistemul obișnuit de poziționare, atunci există probleme:
- Numărul nu se încadrează în gama de calcul tipic [0. 231].
- Costuri de timp pentru reprezentarea unui număr într-un sistem pozițional generalizat.
- Încărcați cantitatea de memorie RAM, dacă numărul este format din liste legate.
În conformitate cu schema reprezentării abstracte a unui număr foarte mare din mai multe cifre (Figura 2), la ieșire se obține un număr foarte mare care nu se încadrează în gama de calcul tipic. Nu este posibilă efectuarea oricăror operații cu un astfel de număr, deoarece este nevoie de sute de pagini de fișiere de orice tip din sistemul de operare Windows.
În acest sens, numerele superimprimate din mai multe cifre A = 22147483648 reprezintă în mod efectiv în sistemul de numere non-poziționare - sistemul de clase reziduale, în care nu există transferuri de la ordinul inferior la cel senior.
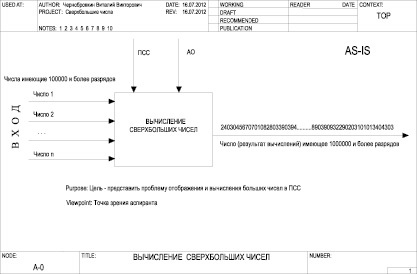
Fig. 1. Schema de calculare a numerelor super-mari
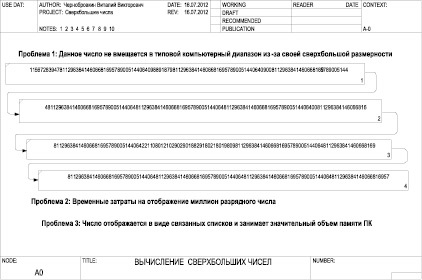
Fig. 2. Schema de reprezentare abstractă a unui număr de mai multe cifre super-mari, sub formă de liste legate
Există o problemă, care este următorul: în cazul în care numărul de super-mare cifră reprezentat printr-un sistem de clase rezidual [5, 7], numărul de resturi, precum și baza de sistem selectat va fi mare, care, la rândul lor, afectează procesele de calcul.
Să introducem domeniul numeric în sistemul de poziție binară [265537. 22147483648].
Declarația 1 Numărul A = 22147483648, care are numărul de biți din intervalul [265537. 22147483648] și mai mult, este posibil să apelați un număr foarte mare din mai multe cifre.
Un număr care are un milion sau mai multe cifre poate fi numit un super-multi-bit, deoarece în execuția reală are o valoare numerică mare.
Exemplul 2 Numerele super-mari din mai multe cifre reprezentate în sistemul de clasă reziduală depind de greutatea poziției | Z | P [1] și, prin urmare, pot consta dintr-un set mare de module selectate și, respectiv, reziduuri. Greutatea rangului de poziție | Z | P depinde de conținutul numărului primelor din acesta. Atunci când se calculează numerele extrem de mari din sistemul de clase reziduale, trebuie luată în considerare următoarea ecuație:
unde A este numărul, rezultatul calculului; - bazele sistemului modular, numere relativ prime.
Aserțiunea 3 Un număr foarte mare poate fi reprezentat cu ajutorul unui sistem de clasă reziduală sub formă de reziduuri de reziduuri [3, 5, 6, 7]
a ≡ b (mod p). (2)
Posibilitatea unei astfel de reprezentări a unui număr este determinată de următoarele teoreme.
Teorema 1 (teorema restului chinezesc) [2, 3, 5, 6, 7].
Orice număr întreg pozitiv din sistemul de clasă reziduală poate fi reprezentat ca un set de reziduuri (deduceri) de la împărțirea acestui număr la bazele (modulele) selectate ale sistemului.
Dovada: Fie numărul A = 22147483648 reprezentat în sistemul de clasă reziduală ca
unde a1, a2, ..., a sunt cele mai mici reziduuri nelegate (reziduuri) formate dintr-o diviziune intregi a numarului A de bazele selectate
unde pi sunt numere relativ prime.
Și dacă această reprezentare a numărului (3) este unică în condiție
Apoi numărul A va arăta astfel:
A ≡ a1 (mod p1);
A ≡ a2 (mod p2); (7)
A ≡ an (mod pn).
Teoremă 2 Dacă numerele în pi = p1, p2. pn sunt perechi coprime, apoi pentru orice reziduuri a1, a2. o astfel încât 0 ≤ an ≤ pn pentru toți i = 1, 2. n există un număr A care, împărțit la pi, dă restul ai pentru toate i = 1, 2. n
Dovada: folosim inducția. Pentru n = 1 teorema este evidentă. Să presupunem că teorema este valabilă pentru n = k - 1; există un număr M care dă restul ri atunci când se împarte cu pi pentru i ∈. Semnificăm prin
d = a1, a2. ak-1. (8)
Luați în considerare numerele M, M + d, M + 2d. M (ak-1) d. Să arătăm că cel puțin unul dintre aceste numere dă restul lui rk când este împărțit de ak. Să presupunem că nu este așa. Deoarece cantitatea de numere egal cu ak și reziduurile posibile pot fi nu mai mult de ak prin împărțirea acestor numere în ak - 1 (din moment ce nici unul dintre numerele nu dă rk reziduu), atunci există două numere cu resturile egale între ele. Lăsați aceste numere
M + sd și M + tdM pentru 0 ≤ s ≤ ak
și 0 ≤ t ≤ ak și s ≠ t. (9)
Atunci diferența lor
(M + sd) - (M + td) = (s - t) d
este împărțită în ak, ceea ce este imposibil, pentru că 0 <s – t Deoarece vorbim de un număr de milioane de cifre, vom descrie problemele reale ale construcției lor în sistemul de clase reziduale: Aceasta înseamnă că, dacă vom construi numere de superimprimare care au un milion sau mai multe cifre, atunci numărul de baze ale sistemului va depinde de cifrele acestor numere. De exemplu, dacă lățimea fiecărei baze selectate este mică, atunci numărul de baze ar trebui să crească în mod corespunzător. Și, dimpotrivă, dacă lățimea bazelor selectate este mare, atunci ele trebuie reduse la numărul necesar. Este vorba despre extinderea sau restrângerea fundamentelor sistemului de clase reziduale [7]. O altă problemă este că atunci când numărul super-mare A = 22147483648 este afișat în sistemul de clasă reziduală, reziduurile pot fi, de asemenea, multi-bit. În cazul general, problemele de mai sus pot fi rezolvate folosind teorema Minor Fermat, dovada căreia este dată în [2, 6] și teorema restului chinez [2, 3, 5, 6, 7]. Punctul principal al teoremei minore a lui Fermat este că dacă p este un număr pozitiv prime și a este un întreg, atunci ap-1 ≡ 1 (mod p) dacă p este un număr prime, (10) apoi ak ≡ ar (mod p) și este suficient să facem calcule numai pentru exponenții a căror exponent este mai mic decât p - 1. Aplicând teorema restului chinez, putem simplifica maparea numerelor super-mari. Arătându-le sub forma reziduurilor de puteri modulo n dacă știm că este prima factorizare. Să presupunem că fiecare factor prim intră în această extindere cu multiplicitatea 1, deoarece în acest caz metoda este cea mai eficientă. Să presupunem că expansiunea are forma unde 0 Pentru numere întregi a și m, vom găsi mai întâi reziduul am pentru fiecare modul pi. Dacă factorii prime nu sunt prea mari, atunci calculele vor fi foarte rapide chiar și pentru m și a mari, deoarece suntem ajutați să facem acest lucru. Teorema lui Fermat (§10). Să presupunem că se fac calcule și am ≡ r1 (mod p1) și 0 ≤ r1 ≤ p1; am ≡ r2 (mod p2) și 0 ≤ r2 ≤ p2; (12) am ≡ rk (mod pk) și 0 ≤ rk ≤ pk. Prin urmare, pentru a determina reziduul am modulo n, trebuie să rezolvăm sistemul congruențelor: Amintiți-vă că modulele sistemului sunt diferite numere primare reciproce. Prin urmare, conform teoremei restului chinez, sistemul are întotdeauna o soluție, de exemplu r, 0 ≤ ri ≤ pi - 1. Mai mult, orice două astfel de soluții sunt congruente modulo p1. pk = n .... Deoarece am este și o soluție a sistemului, avem ≡ r (mod n). Prin urmare, r este un reziduu al lui am modulo n. Un exemplu. Surjectively afișa numărul 22147483648 A = un reziduu selectat baze p1 = 11, p2 = 13, p3 = 17, p4 = 19. Prin schimbarea gradului respectivei numere de unități 2147483648-1 = teorema mică 2147483647 Fermat este cazul, pentru care găsim reziduurile din divizarea gradului 2147483647 (de p-1) din fiecare bază selectată p1, p2, p3, p4. atunci pi-1 = 11 - 1 = 10; pi-2 = 13 - 1 = 12; pi-3 = 17-1 = 16; pi-4 = 19-1 = 18; (14) a'1 = 2147483647 mod 10 = 7; a'2 = 2147483647 mod 12 = 7; (15) a'3 = 2147483647 mod 16 = 15; a'4 = 2147483647 mod 18 = 1. a1 = 22147483647 ≡27 (mod 11); a2 = 22147483647 ≡27 (mod 13); (16) a3 = 22147483647 ≡ 215 (mod 17); a4 = 22147483647 ≡ 21 (mod 19). În cele din urmă, numărul A = 22147483647 va arăta astfel: 27 ≡ 7 (mod 11); 27 ≡ 11 (mod 13); (17) 215 ≡ 9 (mod 17); 2 ≡ 2 (mod 19). 1. reprezentări paralelizare ultralarge numere multibit folosind sistemul claselor reziduale are avantajul de timp pentru calcule, cu o cantitate mare de date care urmează să fie prelucrate, așa cum se realizează procesarea tuturor datelor în paralel și independent. 2. Orice număr din mai multe cifre poate fi reprezentat sub formă de reziduuri din resturile de putere. 3. Calcule paralele accelerate pot fi efectuate pe figuri paralele. 4. Dacă formarea reziduurilor ai este efectuată independent unul de celălalt, fiecare calcul va avea loc și în mod independent unul de celălalt. Inyutin S.A. Doctor în științe tehnice. profesor la departamentul "Proiectarea sistemelor informatice", Universitatea Tehnologică de Stat "FGBOU HPE". KE Tsiolkovsky (MATI), Moscova; Bakharev M.S. Doctor în științe tehnice. Profesor de „Petrol și Gaze de afaceri“ VPO „Surgut Institutul de Petrol si Gaze, Tyumen Petrol Stat și ramura Gaze“ Surgut; Krishtop V.V. Doctor de fizică-matematică. Profesor, șef al Departamentului "Fizică", Universitatea de Stat din Orientul Îndepărtat, Khabarovsk, profesor la Universitatea din Kwangwoon, Coreea. Vă aducem la cunoștință jurnale publicate în editura "Academia de Istorie Naturală" (Factor de impact ridicat al RINC, subiectul jurnalelor acoperă toate domeniile științifice) Jurnal științific ISSN 1812-7339 | ПИ №77-63397 Serviciul de asistență tehnică - [email protected] Secretarul executiv al revistei Bizenkov M.N. - [email protected]
Materialele revistei sunt disponibile sub licența Creative Commons "Attribution" 4.0 World.Articole similare