Metoda de minimizare a funcției cu ajutorul hărților Weich asigură simplitatea obținerii rezultatelor. Se utilizează atunci când se minimizează funcțiile relativ simple (cu numărul de argumente până la cinci). Harta Veitch este o formă definită a tabelului de adevăr. Tabel. 6 sunt harti Weich pentru functiile a doua argumente (a), trei (b) si patru (c), respectiv.
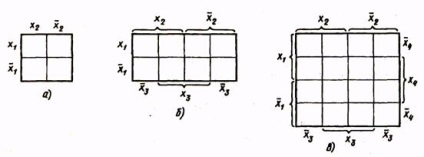
Fiecare celula a hărții corespunde unui anumit set de valori ale argumentelor. Acest set de argumente este determinat prin atribuirea valorii log1 la litere, la intersecția dintre rânduri și coloane ale cărora se află pe celulă. Astfel, în harta funcțiilor a patru argumente (Tabelul 6c), celulele primei linii corespund următoarelor combinații ale semnificațiilor argumentelor:
Numărul de celule de card este egal cu numărul tuturor seturilor posibile de valori ale argumentelor (n este numărul de argumente ale funcțiilor). În fiecare dintre celulele cardului este scrisă valoarea funcției din setul corespunzător de valori ale argumentului. Fie funcția să fie specificată de tabelul de adevăr (Tabelul 7). Tabelul cu adevărat al acestei funcții sub forma hărții Weich este prezentat în Tabelul. 8.
Hartă Weich definește valorile funcției pe toate seturile posibile de valori ale argumentului și este o tabelă de adevăr. Hărțile lui Veich sunt compacte, dar avantajul lor principal este următorul. Cu orice tranziție de la o celulă la alta de-a lungul unei coloane sau rând, valoarea unui singur argument al funcției se schimbă. În consecință, dacă o pereche de celule adiacente conține 1, atunci operația de lipire poate fi efectuată asupra membrilor corespondenți ai formei canonice. Astfel, este mai ușor să căutați membri lipiți.
Tabelul 8 Tabelul 9
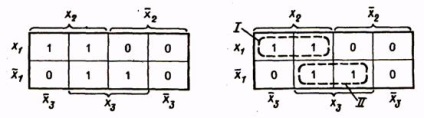
Să formuleze regulile pentru obținerea funcțiilor MDNF cu ajutorul hărților Weich. Toate celulele care conțin 1 sunt combinate în zone închise. În acest caz, fiecare regiune ar trebui să fie un dreptunghi cu un număr de celule 2 k. unde k este 0, 1, 2. Prin urmare, numărul admisibil de celule din regiunea 1, 2, 4, 8. Regiunile se pot intersecta și aceleași celule pot intra în diferite regiuni. Apoi se înregistrează expresia funcției MDNF. Fiecare dintre domeniile din MDNF este reprezentat de un termen al cărui număr de litere de k este mai mic decât numărul total de argumente ale funcției n (adică egal cu). Fiecare membru al MDNF este compus numai din acele argumente care pentru celulele din regiunea corespunzătoare au aceeași valoare (fără inversiune sau cu inversiune).
Astfel, atunci când intră în celulele zone închise trebuie să depună eforturi pentru numărul regiunilor la minimum (numărul minim de membri vor fi în funcție de MDNF), iar fiecare regiune conține cel mai mare număr posibil de celule (în acest caz, ar fi numărul minim de litere în funcția de membri MDNF) .
Considerăm minimizarea cu ajutorul hărții Weich a funcției a trei argumente prezentate în tabel. 9. Toate celulele care conțin 1 sunt acoperite de două regiuni. În fiecare dintre regiunile a câte 2 celule, pentru ele n-k = 3-l = 2, aceste zone din MDNF vor fi reprezentate prin termeni care conțin două litere. Prima zonă corespunde unui termen (argumentul nu este prezent aici, deoarece pentru o celulă din această regiune are o valoare fără inversiune, pentru cealaltă celulă are o inversare); a doua zonă corespunde termenului. În consecință, funcțiile MDNF
Să luăm în considerare un exemplu de minimizare a funcției a patru argumente, set tabel. 10. Prima și a patra regiune au două celule, pentru care n-k-4 -1 = 3. Aceste zone din MDNF vor fi reprezentate de membri care conțin trei litere. A doua și a treia regiune conțin câte patru celule fiecare și în MDNF ele sunt exprimate prin termeni care conțin două litere (n - k = 4 - 2 = 2). Funcția DNP minimă
Tabelul 10 Tabelul 11
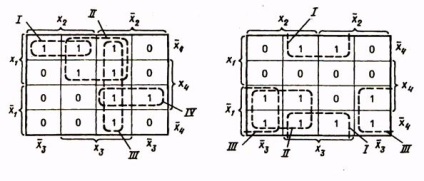
Atunci când se construiește zone închise, este posibilă îndoirea hărții într-un cilindru cu unirea fețelor sale opuse. Din această cauză, celulele extreme ale unui rând sau coloane ale unei mese sunt considerate a fi adiacente și pot fi combinate într-o zonă comună. Prezentăm această tehnică folosind exemplul funcției prezentate în Tabelul. 11. Funcția DNP minimă
Datorită permisiunii unei astfel de hărți pliabile de-a lungul axelor orizontale și verticale, de exemplu: celulele situate în patru colțuri ale hărții funcției a patru variabile se dovedesc a fi vecine și pot fi combinate într-o singură zonă. Arătăm acest lucru prin exemplul minimizării funcției date în Tabelul. 12. Funcția DNP minimă
Tabelul 12 Tabelul 13
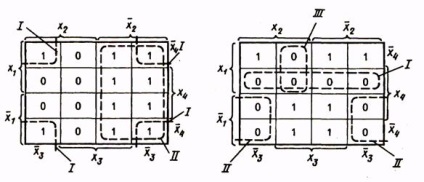
Pentru a obține funcțiile ICNF, zonele închise cuprind celule cu valori zero ale funcției, iar atunci când se scriu termenii expresiei logice, se iau inversiunile argumentelor, la intersecția cărora sunt localizate regiunile. Astfel, pentru funcția dată în tabelul. 13, ICFM
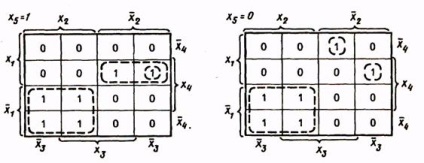
Până acum, am considerat funcții logice cu un număr de argumente până la patru. Reprezentarea unei funcții și minimizarea ei cu ajutorul cardurilor Veich devin mai complicate dacă numărul de argumente este mai mare de patru. În tabel. Figura 14 prezintă o reprezentare a cinci argumente folosind hărțile Weich.
Tabela de adevăr cuprinde două hărți, fiecare dintre acestea reprezentând o hartă a patru variabile. Unul dintre ele corespunde cu x5 = 1, celălalt - x5 = 0. Aceste cărți pot fi așezate mental unul peste altul (figura 3). În acest caz, zonele de acoperire a celulelor pot fi tridimensionale, adică o zonă poate fi acoperită cu celule de două cărți.
Pentru funcția dată în tabelul. 23, MDNF
Pentru a minimiza o funcție cu un număr de argumente mai mari de cinci, hărțile Weich se dovedesc incomod. Minimizarea acestor funcții poate fi efectuată prin metoda Quine.
Generarea paginii: 0.005 sec.