- Și de ce își aminteste de Platon?
- Deoarece Platon a făcut și matematică și a apreciat-o foarte mult. Din lucrările sale, multe date despre știința antică au fost extrase acum. Se crede, de exemplu, că a dat o definiție a conceptului de loc geometric. De altfel, adaug că o parabolă cubică este o curbă importantă în inginerie. De exemplu, atunci când constructorii de cale ferată calculează cursa drumului astfel încât trenul cu viteză ridicată să se aprindă ușor pe șine, atunci această rotunjire trebuie calculată exact prin parabola cubică.
- Încă mai vreau să știu despre înălțimi ", a întrebat Ilyusha. "Este foarte dificil să le definiți?"
- Nu, răspunse Radiks, nu este așa de dificil. Să luăm un exemplu. Să presupunem că există un dreptunghi. Ce ar trebui să iau laturile dreptunghiului astfel încât zona lui să fie cea mai mare dacă suma celor două laturi este egală cu optsprezece?
- Rău înțeleg ceva despre această problemă! - a observat Ilyusha.
- Ascultă, răspunse Radiks, și treptat vei înțelege. Să începem cu asta. Fie ca laturile noastre multiplicatoare să fie a și b, iar suma lor va fi c, adică,
Acum luați pătratele sumelor și diferențelor lor și scădeți unul de celălalt:
Deoarece (a + b) este egal cu c, putem scrie:
ab-c / 4 - (a-b) / 4
Din acest motiv, este clar că deoarece c este o constantă, produsul ab se modifică numai ca o funcție a modificării diferenței (a-b), dar din moment ce pătratul acestei diferențe cu minusul este clar că acest produs este mai mare, cu atât este mai mică valoarea absolută a diferenței a-b). În consecință, produsul a două numere atinge atunci un maxim atunci când valoarea absolută a diferenței lor atinge un minim. Este clar pentru tine?
- Să mergem mai departe! Să numim produsul dorit jocul. Și părți din ea - una va fi X, iar cealaltă.
- Și celălalt va fi optsprezece minus X, - a cerut Ilyusha.
- Așa e. Prin urmare, jocul va fi scris după cum urmează:
Acum luăm diferența factorilor noștri. Noi numim un joc cu un accident vascular cerebral, adică o lovitură de joc:
Deoarece vrem ca jocul-accident vascular cerebral să fie minim, vom căuta ce X ar trebui să fie în cazul în care joc-bar este zero. Și scrie:
Produsul atinge un maxim când o parte este egală cu nouă și, prin urmare, cealaltă este egală cu nouă. Cu alte cuvinte, suprafața maximă a tuturor dreptunghiurilor cu același perimetru are un pătrat. Vom compune un comprimat. În a treia coloană, nu este diferența, ci valoarea absolută a acesteia. Apoi, nouă comprimate nu ar trebui să continue: totul va fi repetat simetric în ordine inversă.
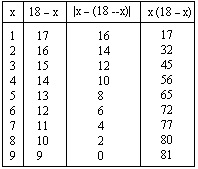
Din ultimele două coloane se observă că atunci când factorii sunt egali, atunci diferența lor este, așa cum era de așteptat, zero, iar produsul lor devine cel mai mare, adică atinge un maxim.
- Deci, a spus Ilyusha. - Într-adevăr, dacă continuați masa și X dați o valoare "zece", atunci celălalt factor va fi egal cu opt și produsul va scădea în ordine inversă. Într-adevăr, maximul!
- Acum, să tragem un grafic al ecuației noastre:
Vedeți că această curbă (și aceasta este o parabolă!) Tocmai trece prin cel mai înalt punct când X este nouă. Ce înseamnă, din punct de vedere geometric, circumstanța că pentru un Xx egal cu nouă, bara de jocuri este zero? Faptul este că bara de joc arată cum se schimbă coeficientul unghiular al tangentei la parabola. Și probabil că vă amintiți că acest coeficient este egal cu tangenta unghiului de înclinare a tangentei în raport cu direcția pozitivă a axei de abscisă? Probabil că-ți amintești că atunci când curba atinge un maxim, atunci tangenta, firește, este localizată.
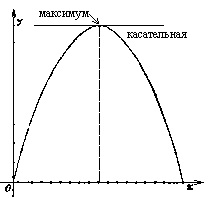
- Paralel cu axa axei X, adică orizontală! - Ilyusha a luat-o.
- Așa este! Acum, spune-mi ce fel de unghi face în acest caz cu axa abscisa?
- Nu formează un unghi!
- Nu. A repetat Radix. "Deci, dacă cineva vă cere să spuneți dacă este cald afară astăzi, atunci vă veți uita la termometrul din afara ferestrei, veți vedea grade zero și veți spune că astăzi nu există temperatură". Deci te înțeleg?
- Nu, - a spus Ilyusha, jenat - desigur, nu poți spune asta. Aici trebuie să spun că acest unghi conține grade zero.
- Doar! răspunse Radiks. "Răspundeți-mi acum, care este tangenta gradelor zero?"
- Ei bine, asta e barul de joc și dă acest lucru foarte zero. Iată cum puteți căuta valori maxime sau minime! Aceasta este una dintre cele mai importante sarcini ale calculului diferențial. Această problemă este foarte mult și fructuos angajată în Fermat și Pascal. Cu toate acestea, sarcina pe care am rezolvat-o acum a fost rezolvată de matematicianul grec Nikomakh în secolul al doilea al erei noastre.
- Dar, de fapt, când matematicienii caută maximul, ei fac și ei același lucru, cum mi-ai arătat acum, sau tocmai l-ai inventat pentru mine?
- Așa au făcut în trecut, de exemplu, în timpul lui Fermat.
Și acum ei fac un pic greșit. Însă sensul acțiunilor este același.
- Și cum se face acest lucru acum?
- Să încercăm să depășim această înțelepciune.
Dacă luăm aceeași funcție și reamintim modul în care am discutat problema convertirii secantului într-o tangență în scholia anterioară, atunci nu va fi atât de dificil să facem față acestei situații. Pentru aceasta avem nevoie, după cum probabil vă amintiți, să cercetați parabola din punctul de vedere al schimbării. Haide, spune-mi: schimb ce?
- Cred că - Ilyusha a răspuns destul de viguros - că va fi o chestiune de schimbare a vitezei cu care crește funcția.
- Așa e. Deci, să începem să studiem schimbarea ratei de schimbare a funcției. În acest scop, oferim o variabilă independentă, adică o creștere, pe care o denotăm cu Δx. Aici Δ nu este un factor, ci cuvântul "increment" care înlocuiește cuvântul "delta", care este citit ca "D" nostru. Iar formula este citită pur și simplu: "delta X".
Creșterea nu este foarte mare, nu foarte mică, dar, în general, finită. Acum, din moment ce x, o variabilă independentă, a primit o creștere (bine, să spunem că avem X egal cu doi și acum vor fi doi și zero zero-trei după punctul zecimal), atunci, deoarece jocul este o variabilă.
- Dependent! l-a îndreptat rapid pe Ilya. -. și, prin urmare, ar trebui să fie și ea. Și ce?
- De asemenea, va crește.
- Răspunsul este demn. Și vom numi acest increment Ay, adică "delta york". Când găsim creșteri, luăm atitudinea lor. Dacă toate acestea sunt descrise în desen, atunci este ușor să vedem că se obține același triunghi dreptunghic drept caracteristic remarcabil Pascalov pe care l-ați văzut pe pagină. (nu confunda acest triunghi Paskalev cu un alt triunghi binomic Paskalev, care a fost discutat în Șapte Șapte!