2.2. Simularea prin schema proceselor Markov continue
Există o clasă largă de sisteme care își schimbă stările în momente aleatorii. Ca și în cazul precedent, în aceste sisteme este luat în considerare un proces cu stări discrete. De exemplu, trecerea unui obiect de la o stare sănătoasă la una defectuoasă, corelarea forțelor părților în timpul bătăliei etc. Evaluarea eficacității unor astfel de sisteme este determinată prin utilizarea probabilităților fiecărui stat în orice moment.
Pentru a determina probabilitatea stării sistemului pentru orice moment de timp, este necesar să se utilizeze modele matematice ale proceselor Markov cu timp continuu (procese Markov continue).
În simularea sistemelor cu procese continue Markov, nu putem profita de probabilităților de tranziție, deoarece probabilitatea de „salt“ de la un stat la altul exact la momentul zero (probabilitatea de orice valoare particulară a unei variabile aleatoare continue).
Prin urmare, în loc de probabilitățile de tranziție, introducem densitatea de probabilitate a tranzițiilor:
unde este probabilitatea ca un sistem care a fost într-o stare într-un moment într-un stat să intre într-un stat.
Până la ordinea a doua infinitezimală, este posibil să se reprezinte din formula de mai sus:
Un proces Markov continuu se numește omogen dacă densitatea de probabilitate a tranzițiilor este independentă de timp (de la momentul începerii intervalului). Altfel, se spune că un proces Markov continuu este neomogen.
Scopul simulării. ca și în cazul proceselor discrete, este determinarea probabilităților statelor sistemului. Aceste probabilități se găsesc prin integrarea sistemului Kolmogorov al ecuațiilor diferențiale.
Să formuleze tehnica de modelare prin schema proceselor Markov continue.
- Determinați starea sistemului și densitatea de probabilitate a tranzițiilor.
- Creați și marcați un grafic de stare.
- Construiește un sistem al ecuațiilor diferențiale ale lui Kolmogorov. Numărul de ecuații din sistem este egal cu numărul de stări. Fiecare ecuație se formează după cum urmează.
- În partea stângă a ecuației, este scris derivatul stării de probabilitate.
- În partea dreaptă se scrie suma algebrică a produselor u. Numărul de produse este la fel de mult ca săgețile asociate cu această stare. Dacă săgeata graficului este direcționată către această stare, atunci produsul corespunzător are un semn plus, dacă din starea dată este minus.
- Definiți condițiile inițiale și rezolvați sistemul de ecuații diferențiale.
Exemplul 2.2. Pentru a crea un sistem de ecuații diferențiale Kolmogorov pentru a găsi probabilitățile stărilor sistemului, graficul de stare marcat al acestora este prezentat în Fig. 2.3.
Fig. 2.3. Graful de stare marcat
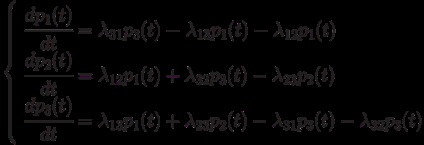
Prin urmare, oricare dintre primele trei ecuații poate fi eliminată ca una liniară dependentă.
Pentru a rezolva ecuațiile Kolmogorov, este necesar să se stabilească condițiile inițiale. Pentru exemplul 2.2 considerat, se pot defini condițiile inițiale:.
Când se investighează obiecte complexe, este întotdeauna de interes: este regimul staționar (staționar) posibil în sistemul investigat? Asta este, cum se comporta sistemul când? Există valori limită? De regulă, aceste valori limită sunt de interes pentru cercetător.
Răspunsul la această întrebare este dat de teorema lui Markov.
Dacă pentru un proces Markov discret omogen, cu un număr total de state finit sau numărare, atunci valorile limită există și valorile lor nu depind de starea inițială aleasă a sistemului.
În ceea ce privește continuu Markov procesele teorema lui Markov este interpretat după cum urmează: în cazul în care procesul este uniformă și o tranziție de la fiecare stat într-un timp finit pentru orice alt stat, iar numărul de stări este numărabil sau finit, valorile limită există și valorile lor nu depind de starea inițială.
De exemplu (Figura 2.4), există un mod staționar în sistemul A, dar în sistemul B nu există nici un mod staționar: dacă sistemul este într-o stare, nu poate merge în nici o altă stare.
click pentru a mari imaginea
Fig. 2.4. Exemple de grafice de stare ale sistemelor cu moduri diferite
2.3. Schema de deces și reproducere
Adesea, în sisteme de diferite scopuri, apar procese care pot fi reprezentate ca un model de "moarte și reproducere".
Graficul grafic al stărilor unui astfel de proces este prezentat în Fig. 2.5.
Particularitatea modelului este prezența relațiilor directe și inverse cu fiecare stat învecinat pentru toate statele medii; Primul și ultimul (extrem) stări sunt asociate numai cu un "vecin" (cu stările ulterioare și anterioare, respectiv).
Numele modelului - „naștere și moarte“ - este asociat cu ideea că săgeata din dreapta pentru a indica trecerea la starea asociată cu creșterea numărului de stat ( „naștere“), și săgețile din stânga - cu o scădere a numărului de stări ( „moarte“).
Evident, în acest proces există o stare staționară. Nu este necesară formularea ecuației Kolmogorov, deoarece structura este regulată, formulele necesare sunt date atât în cărțile de referință, cât și în literatura recomandată.
Pentru cele prezentate în Fig. 2.5 desemnările formulei au forma:
Exemplul 2.3. Există un sistem de două computere identice și paralele.
Este necesar să se determine caracteristicile de fiabilitate ale acestui sistem.