Definiția. Să presupunem că în plan sunt date o linie dreaptă a și două puncte A și B. Aceste puncte sunt numite simetrice dacă:
2) linia dreaptă a împarte segmentul în jumătate (figura 9).
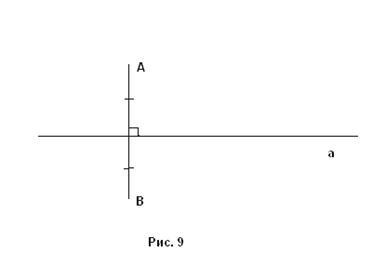
Linia dreaptă a se numește axa simetriei.
Definiția. Cartografierea unui plan în sine se numește simetrie în jurul axei a sau a unei simetrii axiale dacă fiecare punct A al planului este pus în corespondență cu punctul simetric A1 pe axa a.
Proprietățile simetriei axiale:
1). Pentru simetrie axială, linia merge drept;
2). Pentru simetrie axială, segmentul trece într-un segment egal;
3). Pentru simetrie axială, unghiul devine egal cu unghiul său;
4). Simetria axială este mișcarea.
Să luăm în considerare exemple de aplicare a simetriei.
Exemplul 6. Având în vedere o linie dreaptă k și două puncte A și B care nu se află pe această linie. Pe k, găsiți un punct X astfel încât suma AX + XB să fie minimă.
Analiză. Să presupunem că problema este rezolvată. Dacă punctele A și B se află pe laturile opuse ale K, atunci este evident că X este punctul de intersecție al segmentului AB și linia k. Dacă punctele A și B se află pe o parte a lui k, atunci mapând B simetric în raport cu k, obținem un punct B1 astfel încât XB = XB1 și, prin urmare, punctul X trebuie să se afle pe segmentul AB1 (Figura 10).
Clădire. Dacă punctele A și B se află pe laturile opuse ale k, atunci tragem segmentul AB și intersecția cu k este punctul cerut al lui X.
Dacă A și B sunt pe o parte a lui k, atunci mapând B simetric în raport cu k, obținem punctul B1. Desenând segmentul AB, obținem punctul dorit X.
Dovada. În primul caz dovada este evidentă. În al doilea caz, atunci când A și B, pe de o parte a k: să Y - orice alt punct al liniei k, diferit de H. Apoi, din proprietățile de simetrie vedem că Y BY = B1, iar inegalitatea triunghiului avem AY + YB = = AY + YB1> AB = AX + XB1 (figura 10).
Studiu. Problema are o soluție în orice moment și un singur lucru.
Exemplul 7. Construiește un ABCD patrulaterar dacă sunt date segmentele care sunt laturile AB = a, BC = b, Cd = c, A = d și se știe că diagonala AC împarte unghiul A în jumătate (Figura 11).
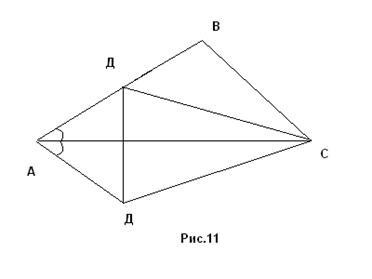
Analiză. Să presupunem că problema este rezolvată, iar ABCD cvadrilateral este cea dorită. Apoi de pe ambele părți AB și AD încă o dată. Pentru caracterul definitoriu lăsați a> d. Dacă reprezentăm punctul A relativ la linia AS simetric, obținem punctul Ai pe partea AB. În triunghiul BCD1, toate laturile sale sunt cunoscute: BC = b, SD = c, D1 B = a - d. Astfel este construit triunghiul D1 î.Hr., iar apoi întregul patrulater este construit.
Clădire. Construim triunghiul A1 al BC de-a lungul celor trei laturi BC = b, Cd = c, A, B = a - d. Apoi vom continua partea VD1 dincolo de punctul D1 și din B vom compila segmentul AB = a, obținem punctul A. Construim punctul A, simetric cu punctul A, în raport cu AC. Legăm punctele A și D, D și C. ABCD quadrilateral este cel dorit.
Dovada. Evident, din construcții.
Analiză. Construcția este posibilă dacă este posibil să se construiască un triunghi D1 BC, adică inegalitățile triunghiului b <с + а + d, с <в + а – d, а – d <в + с. В этом случае задача имеет одно решение.