Graficul oscilației armonice
Oscilațiile armonice joacă un rol important în fizică. Sarcina noastră este să construim grafice de oscilații armonice în cazuri speciale și să repetăm toate regulile transformării diagramelor cunoscute.
Harmonizările oscilante respectă următoarea lege:
ciclic (circular) de frecvență,
faza inițială de oscilație, de obicei
Perioada de oscilații armonice poate fi calculată din formula
Luăm un caz special de oscilații armonice și aplicăm toate regulile de transformare a grafurilor cunoscute.
Problema 1. Construiți un grafic al oscilațiilor armonice
Indicăm imediat o eroare tipică în astfel de probleme: trecerea la o se face pe
Cum să construiți un program pentru această fluctuație? Etapele de construcție sunt după cum urmează:
1. Funcția inițială.
2. Compresie de 2 ori față de axa y.
3. Întinderea este de 2 ori față de axa x (Figura 1).
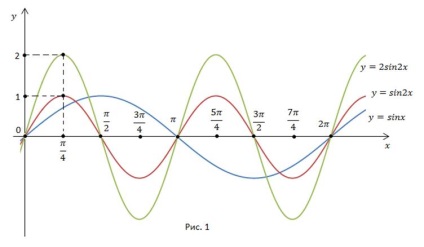
4. Deplasați-vă spre dreapta de-a lungul axei x (Figura 2).
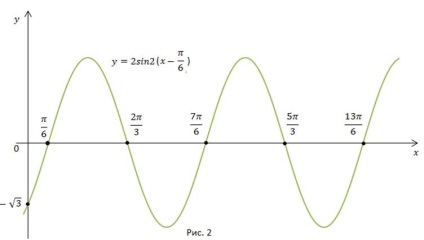
În construirea acestui grafic, a fost utilizată transformarea principală a graficelor:
Sarcina 2. Construiți graficele funcțiilor:
a) Găsim perioada funcției
Perioada înseamnă suficient pentru a compune parcela pe parcelă. Prin împărțirea acestei secțiuni în 4 intervale egale, obținem punctele care determină comportamentul graficului: (Figura 3).
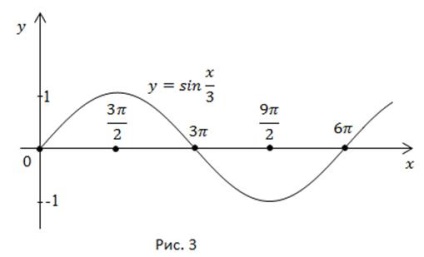
b) Găsim perioada funcției
Să construim un grafic pe un segment cu o lungime într-o perioadă. Să îl împărțim în 4 intervale egale și să obținem punctele (figura 4).
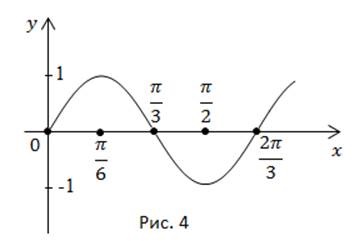
Puteți verifica corectitudinea plotării prin găsirea valorilor funcției la anumite puncte.
Am construit grafice de funcții folosind periodicitatea. De asemenea, s-ar putea construi o jumătate de undă și o vom mapa în întregul domeniu al definiției.
Sarcina 3. Construiți graficele funcțiilor:
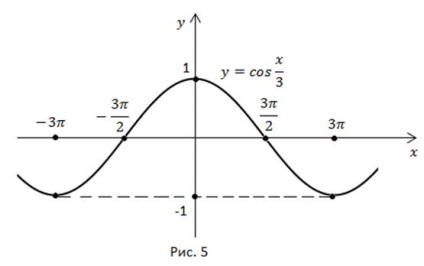
Cosinul este o funcție uniformă, astfel încât să putem compune complotul pe o parcelă egală. În acest interval, funcția scade monotonic de la la. Am mapat simetric graficul graficului în raport cu axa y și obținem un grafic al funcției pe întreaga lungime a perioadei: (figura 5).
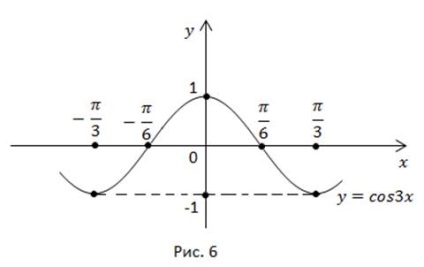
Cosinul este o funcție uniformă, trasăm complotul pe un segment apoi mapat simetric pe axa y și obținem un grafic pe un interval a cărui lungime este egală cu perioada (Figura 6).
Am analizat graficul oscilațiilor armonice. Vedem că pentru a construi un grafic de oscilație armonică este necesar să supuneți curba inițială transformărilor cunoscute: comprimare, întindere, forfecare. Mastering aceste reguli este utilă în construirea altor grafice.