Un giroscop este un corp cu rotație rapidă a cărui axă de rotație își poate schimba poziția în spațiu. De obicei, unul dintre punctele axei giroscoapelor este fixat, se numește punctul de susținere a giroscopului.
Gyro numit liber dacă nici o forță externă este zero (= 0), iar în cazul în care centrul de masă coincide cu punctul de sprijin. Cea mai mare valoare în domeniul științei și tehnologiei au giroscoape simetrice cu simetrie de rotație în jurul unei axe, numit geometrice axa giroscopului sau giroscoapelor axa de simetrie.
Când momentul forțelor exterioare este egal cu zero, impulsul angular al giroscopului rămâne neschimbat. Astfel, dacă giroscopul este condus într-o rotație rapidă în raport cu axa sa de simetrie, atunci axa giroscopică nu trebuie să-și schimbe poziția în spațiu.
Giroscopul constă dintr-un rotor (corpul unui giroscop rotindu-se în raport cu axa sa de simetrie) și un sistem de inele numit suspensie cardanică. Suspensia cardanică vă permite să localizați rotorul giroscopic astfel încât axa acestuia să poată ocupa orice poziție în spațiu.
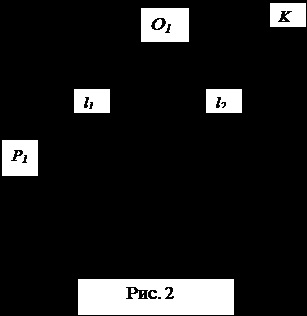
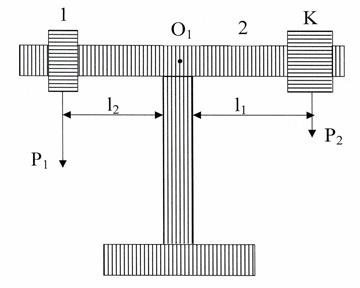
Dacă balansăm giroscopul cu contrabalansarea K, atunci momentul rezultat al forțelor care acționează asupra sistemului va fi zero, adică:
unde P1 este gravitatea rotorului față de axa giroscopică, P2 este gravitatea contragreutății.
Giroscopul are un moment unghiular constant L. care coincide în direcția cu viteza unghiulară. Astfel, în absența unui moment de forțe externe, giroscopul își păstrează poziția axei sale în spațiu.
Dacă deplasați contragreutatea la o mică distanță de poziția de echilibru, centrul de greutate al sistemului se va deplasa în punctul O2 (Figura 3). Echilibrul este încălcat și axa giroscopului se înclină într-un unghi # 966 ;.
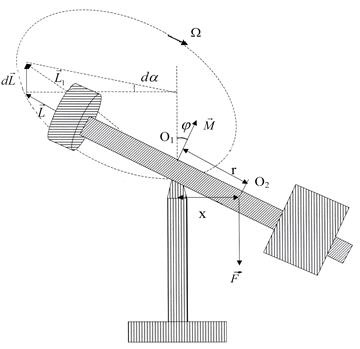
Aceasta înseamnă că axa giroscopului își va schimba poziția în spațiu prin rotirea timpului dt cu unghiul d # 945;. În următoarea perioadă de timp dt, o modificare a momentului unghiular va apărea din nou cu o sumă etc. Drept urmare, axa giroscopului se va roti continuu la o anumită viteză unghiulară # 937; O astfel de mișcare este numită procesiune. valoare
se numește viteza unghiulară a procesiunii. Din fig. 3 că dL = Ld # 945; prin urmare, ecuația (2.8) poate fi scrisă în formular
Astfel, viteza unghiulară de rotație a giroscopului față de axa verticală (viteza unghiulară a procesiunii) este direct proporțională cu momentul forței și invers proporțională cu impulsul unghiular.
În cazul general, legătura dintre. și este exprimată prin ecuația: