Difracția de la o gaură rotundă. Să luăm în considerare difracția în raze convergente sau difracția Fresnel, care apare atunci când modelul de difracție este observat la o distanță finită de obstacolul care a cauzat difracția.
Am pus în calea unui val de lumină sferică un ecran opac cu o gaură circulară de rază. Ecranul este poziționat astfel încât perpendicula care a scăzut de la S pe ecranul opac să cadă exact în centrul găurii (Figura 17.13).
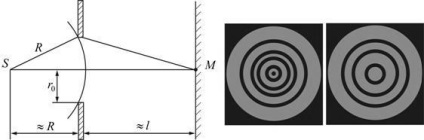
Cu privire la continuarea acestei perpendiculare luăm punctul M și luăm în considerare ce vom observa pe ecran.
Împărțim partea deschisă a suprafeței undei în zonele Fresnel. Forma modelului de difracție depinde de numărul de zone Fresnel deschise de gaură. Amplitudinea oscilației rezultate, excitată la punctul M de toate zonele
Astfel, atunci când gaura deschide un număr impar de zone Fresnel, amplitudinea (intensitatea) la punctul M va fi mai mare decât atunci când valul se propagă liber; dacă nici măcar. atunci amplitudinea (intensitatea) va fi zero, după cum se arată în Fig. 17.13.
Bineînțeles, dacă. atunci nu va fi nici un model de difracție.
Difracția de pe disc. Un val sferic propagând dintr-o sursă punctuală S. întâlnește un disc în calea sa (Figura 17.14).
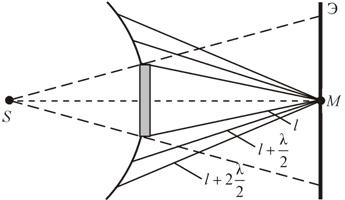

Punctul M se află pe perpendicular pe centrul discului. Prima zonă Fresnel este construită de la marginea discului și așa mai departe.
Amplitudinea oscilațiilor luminoase la punctul M este egală cu jumătate din amplitudinea datorată primei zone deschise. Dacă dimensiunea discului este mică (acoperă un număr mic de zone), atunci acțiunea primei zone diferă foarte puțin de acțiunea zonei centrale a cadrului. Astfel, iluminarea la punctul M va fi la fel ca în absența unui ecran. Datorită simetriei, punctul central al luminii va fi înconjurat de inele de lumină și de umbră (în afara limitelor umbrei geometrice).
Paradoxal, la prima vedere, concluzia, în virtutea căruia, în centrul umbrei geometrice ar putea fi un punct luminos a fost făcută de Poisson în 1818 și a fost ulterior numit după el. "Poisson Blot" confirmă corectitudinea teoriei lui Fresnel.
17,7. Difracția în grinzi paralele (Fraunhofer Diffraction)
Tipul de difracție, în care modelul de difracție este format din grinzi paralele. se numește difractă Fraunhofer. Radiații paralele vor apărea dacă sursa și ecranul sunt la infinit. Practic se folosesc două obiective: una se concentrează pe sursa de lumină, iar cealaltă focalizează ecranul.
Cu toate că, în principiu, de difracție Fraunhofer nu diferă de difracție Fresnel, dar, în practică, acest lucru este cazul este important deoarece este acest tip de difracție este utilizat în mai multe dispozitive de difracție (cu rețea de difracție, de exemplu). În plus, există un calcul matematic mai ușor și ne permite să rezolve problema înainte de sfârșitul cantitativă (difracție Fresnel, am considerat calitativ).
Difracția luminii pe o singură fantă. Să existe un spațiu în ecranul continuu: lățimea fantei. lungimea fantei (perpendiculară pe planul foii) (figura 17.15). Radiațiile paralele de lumină cad pe fanta. Pentru a facilita calculul, presupunem că în planul decalajului AV amplitudinile și fazele undelor incidente sunt aceleași. Împărțim diferența în zonele Fresnel, astfel încât diferența de cale optică dintre razele care vin din zonele învecinate este egală cu.
În cazul în care un număr uniform de astfel de zone sunt așezate pe lățimea fantei, atunci se va observa o intensitate minimă în punctul (focalizarea laterală a cristalinului) și dacă există un număr impar de zone, atunci intensitatea maximă:
- condiția de intensitate minimă;