2.4 SOLUȚIONAREA PROBLEMELOR PE TEMA "PRESIUNE HIDROSTATICĂ"
Numărul sarcinii 1. Coborâți degetul într-un pahar de apă, fără a atinge fundul geamului. Se schimbă forța presiunii apei în partea de jos? Dacă se schimbă, cum?
Soluția: Presiunea lichidului de pe fundul vasului depinde de nivelul lichidului din vas. Dacă inițial sticla nu a fost umplută la vârf, atunci după scăderea degetului, nivelul apei va crește, ca urmare, forța de presiune către fund va crește. Dacă sticla a fost umplută la vârf, forța de presiune de pe fund nu se va schimba (o parte din apă se va revărsa pur și simplu din sticlă).
Numărul sarcinilor 2. Se va schimba presiunea apei în partea inferioară a găleată dacă mingea este coborâtă în apă? Piatra?
Notă: Presiunea va crește dacă galeata este incompletă și va rămâne neschimbată în cazul în care găleata a fost umplută cu apă în partea superioară.
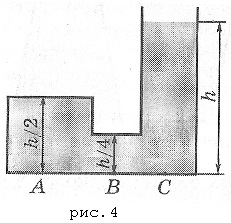
Numărul sarcinii 3. Care este presiunea apei în partea de jos la punctele A, B, C (figura 4)? Presiunea atmosferică nu este luată în considerare.
P
W
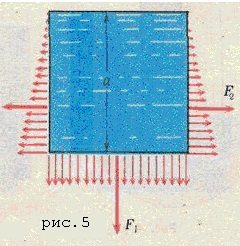
Presiunea lichidului de pe fundul vasului va fi egală cu greutatea coloanei de lichid de înălțime a cu suprafața de bază egală cu unitatea:
Forța de presiune pe fundul vasului:
Presiunea pe fața laterală a cubului va depinde de distanța față de suprafața lichidului. La o adâncime h, presiunea
Deoarece presiunea variază liniar cu adâncimea, pentru a determina forța de presiune avem nevoie de o presiune medie
se înmulțește cu suprafața laterală:
Numărul sarcinii 5. Pe foaia de cauciuc orizontală este inversat raza pan R = 10 cm și o înălțime H = 15 cm. Fundul oalei forate orificiul circular cu raza R = 1 cm, care este bine introdus un tub de lumină vertical (Fig. 6). În tigaie, prin tubul se toarnă apă. Când apa umple oala si se ridica prin tubul de la h = 4 cm, începe să curgă de sub marginile tigaie. Care este masa m de tigaie?
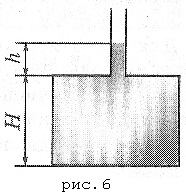
Soluția: Apa începe să curgă când tigaia este ușor ridicată. Ridichează presiunea în sus a vasului în sus. Această forță
trebuie să echilibreze greutatea mg care acționează pe tava. Aici p = ρgh este presiunea apei la fund,
- zona inferioară a tăvii (luând în considerare gaura).
Din condiția de echilibru F = mg găsim
Rețineți că răspunsul nu depinde de înălțimea panului H.
Numărul sarcinii 6. Estimați masa atmosferei Pământului (raza Pământului = 6400 km).
Soluția. Greutatea atmosferei este egală cu forța presiunii aerului pe întreaga suprafață a Pământului, a cărei suprafață este
Această valoare este mai mică de o milionime din masa totală a planetei noastre. O estimare simplă a masei atmosferei este posibilă deoarece partea principală a atmosferei este concentrată la altitudini mici în comparație cu raza Pământului. Prin urmare, putem presupune că greutatea atmosferei este de mg. unde g este accelerația gravitației în apropierea suprafeței Pământului.
2.5 STUDIUL TEMEI "NAVELE DE MESAJ"
Proprietatea unui fluid care transmite presiunea în toate direcțiile fără alterare face posibilă explicarea structurii vaselor comunicante.
Navele care au o parte comună (care le conectează), umplută cu un lichid de odihnă, se numește comunicare.
P
P
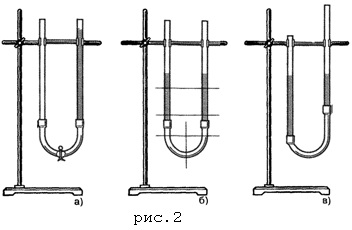
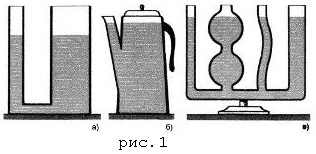
Legea comunicării vaselor: în cazul vaselor de comunicații, suprafețele unui fluid omogen sunt stabilite la același nivel.
Pentru a dovedi această lege, să luăm în considerare particulele de lichid situate în locul unde se conectează vasele (în partea inferioară din figura 1a). Deoarece aceste particule (împreună cu restul lichidului) sunt în repaus, forțele de presiune care acționează asupra lor din stânga și din dreapta trebuie să se echilibreze reciproc. Dar aceste forțe sunt proporționale cu presiunile, iar presiunile sunt la înălțimea stâlpilor de lichid pe a căror parte acționează aceste forțe. Prin urmare, din egalitatea forțelor luate în considerare, urmează și egalitatea înălțimilor coloanelor lichide din navele comunicante.
și
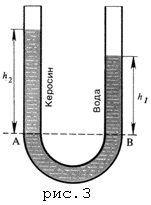
Acest lucru se datorează faptului că presiunea lichidului de pe fundul vasului depinde nu numai de înălțimea coloanei, ci și de densitatea lichidului. Deoarece lichidul în acest caz se va odihni, este încă posibil să se afirme că presiunea generată și din dreapta și stânga stâlpi de lichide (de exemplu, la nivelul AB în figura 3), egală cu:
Exprimăm fiecare dintre presiuni folosind formula de presiune hidrostatică:
Din această egalitate rezultă că în vasele de comunicare înălțimile coloanelor de lichid deasupra nivelului de separare a lichidelor sunt invers proporționale cu densitatea acestor lichide. Înălțimile coloanelor lichide sunt contorizate de pe suprafața de contact a lichidelor unul cu celălalt.
2.6 SOLUȚIONAREA SARCINILOR CU PRIVIRE LA TEMA "MESAJAREA NAVELOR"
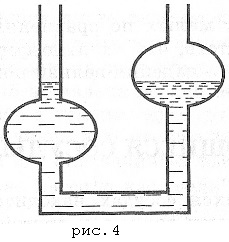
Numărul sarcinii 1. Mercurul se găsește în vasele comunicante. În unul dintre vase, se adaugă apă, iar în cealaltă - kerosen. Înălțimea coloanei de apă hv = 20 cm. Care ar trebui să fie înălțimea h a coloanei de kerosen, astfel încât nivelurile de mercur din cele două recipiente să coincidă?
Soluția. Nivelele de mercur vor coincide dacă presiunea coloanei de apă și a coloanei de kerosen este aceeași: ρвghв = ρкghк. De aici găsim hk = ρvhv / ρk = 25 cm.
W
Soluția. După izolarea unei secțiuni în tubul de conectare. La început, presiunea apei pe această secțiune de pe ambele părți era aceeași, iar apa nu se mișca. Cu aceeași scădere a densității apei în vase, creșterea înălțimii coloanelor de apă din ele va fi diferită. În vasul stâng, înălțimea coloanei de apă va crește mai repede decât în cea dreaptă. Deoarece presiunea apei este proporțională cu înălțimea coloanei, presiunea din partea stângă a zonei dedicate va fi mai mare și apa din tubul de conectare va începe să se deplaseze spre dreapta.
Numărul sarcinii 3. La echilibru, pistonul din primul vas de comunicare (Figura 5) este setat la h1 = 20 cm mai mare decât în cel de-al doilea. Masa pistonului m1 = 2 kg și m2 = 4 kg. Dacă punem o greutate de m3 = 3 kg pe primul piston, pistoanele vor fi instalate la aceeași înălțime. Cum vor fi aranjate pistoanele dacă greutatea este rearanjată la al doilea piston?
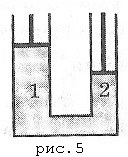
Soluția. În această sarcină, nu putem presupune că forțele de presiune de fluid pe pistoane sunt ambele zone ale pistoanelor, atunci când pistoanele sunt stabilite la niveluri diferite, ar trebui să ia în considerare presiunea coloanei de lichid. Dacă mutați greutatea în cel de-al doilea piston, acesta va fi mai mic decât primul. Denotând diferența de înălțime a pistoanelor în acest caz h. ρ densitatea de lichid, iar zonele S1 și S2 ale pistoanelor și având în vedere faptul că forța de presiune a fluidului asupra pistonului este în modul de echilibru al greutății pistonului cu sarcina, obținem sistemul de ecuații:
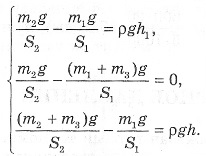
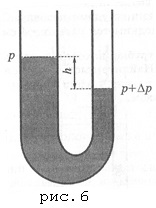
Numărul sarcinii 4. Tuburile manometrului în formă de U de mercur au diametre diferite. La care dintre manometrele trebuie conectat un vas în care trebuie măsurată presiunea, astfel încât precizia de măsurare să fie mai mare? (Scala este atașată la cotul îngust al manometrului).
P
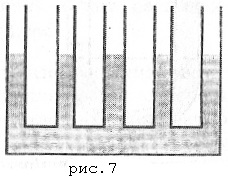
Numărul sarcinii 5. Cinci nave de comunicare identice (figura 7) sunt umplute parțial cu apă. Un strat de kerosen cu o înălțime h = 25 cm este adăugat la unul dintre recipiente. Cât va crește nivelul apei în restul vaselor?
P
Numărul sarcinii 6. În tubul în formă de U există mercur, apă și kerosen (figura 8). Găsiți înălțimea coloanelor de apă și kerosen dacă nivelul de mercur din genunchiul drept al tubului este h = 1 cm mai mare decât cel din stânga.
Soluția. Lăsați înălțimea coloanei de kerosen (figura 9) hc. atunci înălțimea coloanei de apă este hb = hk + h. Presiunea la punctele A și B ar trebui să fie aceleași: hk = h (ρrt -ρv) / (ρv -ρk) = 63 cm Prin urmare, h = 64 cm ..