K-gruparea mediană și măsurarea distanței asimetrice
De obicei, un standard de grupare k înseamnă distanța euclidiană este destul de mult, dar aici ne confruntăm cu câteva probleme care sunt adesea întâlnite în gruparea de date, cu o răspândire mare (fie că este vorba de vânzare cu amănuntul, dacă clasificarea textelor sau a bioinformatica).
Folosind gruparea k-mediană
Prima problemă evidentă este că centrele dvs. de cluster sunt exprimate în zeci de unități, în timp ce vectorul de tranzacție al fiecărui client este exact zero sau unul. Ce inseamna cu adevarat pentru tranzactie? Vreau centrele de cluster să exprime fie tranzacția, fie absența ei!
Dacă schimbați ușor algoritmul de grupare astfel încât acesta să utilizeze numai valorile vectorilor de tranzacție ai cumpărătorilor, atunci el va fi deja numit clustering de k-mediians și nu by k-means.
Și dacă nu doriți să schimbați distanțele euclidane, atunci tot ce aveți nevoie este să adăugați o condiție binară (bin) în "Căutarea de soluții" pentru toate centrele de cluster.
Dar dacă centrele de cluster sunt acum binare, atunci cum să folosiți distanța euclidiană?
Mergem la măsurarea corespunzătoare a distanțelor
Trecerea de la k-mijloace la k-mediani, oamenii de obicei nu mai folosesc distanța euclidiană și încep să folosească ceva numit distanța Manhattan sau metrica din cartierul urban.
În ciuda faptului că distanța de la punctul A la punctul B se măsoară într-o linie dreaptă, un taxi din Manhattan au pentru a naviga printr-o rețea de străzi drepte, în cazul în care traficul poate doar la nord, sud, est sau vest. Prin urmare, dacă în Fig. 2-13 vedeți că distanța dintre dansatoare-elev și centrul său cluster este de aproximativ 4,47, acesta din Manhattan distanța este egală cu 6 metri (4 m + 2 metri lateral în jos).
În ceea ce privește datele binare, cum ar fi datele de vânzări, distanța Manhattan între centrul clusterului și vectorul client este pur și simplu numărul de neconcordanțe. În cazul în care centrul clusterului 0 și I 0, distanța în această direcție este 0, iar dacă există 0 sau 1, adică, numerele nu se potrivesc, atunci direcția distanța este egală cu 1. Adăugarea de ei, veți obține distanța totală, care este pur și simplu numărul discrepanțelor.
Este distanța de la Manhattan jucând un rol-cheie în decizie?
Ce înseamnă "cumpărătorul a făcut o înțelegere"? Acest lucru înseamnă că el a vrut cu adevărat să cumpere acest produs!
Ce înseamnă "cumpărătorul nu a făcut o înțelegere"? Acest lucru înseamnă că el nu a vrut acest produs la fel de mult cum a vrut pe cel pe care la cumpărat? Sunt semnale pozitive și negative puternice? Poate îi place șampania, dar deține deja un stoc în subsol. Poate că nu ți-a văzut buletinul informativ pentru luna asta. Există multe motive pentru care cineva nu face ceva, ci doar câteva - de ce se desfășoară acțiunile.
Cu alte cuvinte, merită atenția la ordine, și nu la absența lor.
Există un cuvânt complicat - "asimetria" datelor. Unitățile sunt mai valoroase decât zerouri. Dacă un cumpărător coincide cu altul în trei unități, atunci acesta este un meci mai important decât cel al celui de-al treilea cumpărător pentru trei zerouri. Ceea ce vă atrage atenția - deci este un număr mic de unități de valoare în date - aici sunt "date rare"!
Trebuie să calculați distanța asimetrică. Și pentru variabilele din cod binar, cum ar fi aceste comenzi de vin, există o mulțime de opțiuni bune.
Metoda cea mai probabil utilizată pentru calcularea distanței asimetrice pentru datele formatului 0-1 este numită distanța cosinus.
Distanța de cosinus - nu este atât de înfricoșător, în ciuda trigonometriei
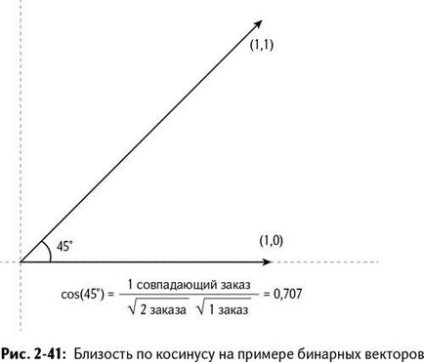
Cea mai simplă modalitate de a explica distanța cosinusului este de a analiza noțiunea de "proximitate cosinus".
Luați în considerare o pereche de vectori binari bidimensionali (1,1) și (1,0). În primul vector, ambele mărfuri au fost comandate, în timp ce în al doilea numai primul. Puteți să reprezentați acești vectori în spațiu și să vedeți că unghiul dintre ele este de 45 de grade (Figura 2-41). Ia protractorul - verifică.
Putem spune că apropierea lor este cosinus de 45 de grade, care este de 0.707. Dar de ce?
Se pare că cosinusul unghiului dintre două ordine binare este:
Numărul de ordine în două vectori, împărțit la produsul rădăcinilor pătrate a numărului de ordine ale primului și al doilea vector
În cazul nostru, cei doi vectori (1,1) și (1,0) au un ordin de potrivire, astfel încât numărătorul este 1 și numitorul - rădăcina pătrată a două (2 tranzacție încheiată) înmulțită cu rădăcina pătrată a unuia din afacere. Ca rezultat, avem 0.707 (figura 2-41).
Ce este remarcabil cu privire la acest calcul?
• contorul din formula se referă numai la coincidențele tranzacțiilor, adică este asimetric și, prin urmare, se potrivește perfect cu acest caz;
• rădăcina pătrată a numărului de tranzacții pentru fiecare vector în numitorul atrag atenția asupra faptului că vectorul, care a comis toate tranzacțiile - să o numim ilizibile - o mult mai îndepărtată de pe celălalt vector decât cea care a comis aceeași tranzacție și nu sunt comise mai multe altele. Ai nevoie pentru a se potrivi vectori, „gusturi“, care sunt la fel, și nu un singur vector care conține un „gust“, pe de altă parte.
• pentru date binare, această apropiere se situează în intervalul între 0 și 1 și doi vectori nu primesc 1 până când toate ordinele lor se potrivesc. Aceasta înseamnă că proximitatea 1-cosinus poate fi folosită ca o măsură a distanței, numită distanța cosinus, care de asemenea variază de la 0 la 1.
Și acum totul este același, dar în Excel
Este timpul să dați șansa de a demonstra clusterizarea k-mediană cu ajutorul distanței cosinus.
Clusteringul cu distanța cosinusului este, de asemenea, denumit uneori ca o k-medie sferică. În capitolul 10 veți vedea k-mijloace sferice în R.
Vom fi consecvenți și vom continua cu k = 5.
Din nou, începeți să copiați foaia de 5MS și să o redenumiți, de data aceasta în 5MedC. Deoarece centrele de cluster ar trebui să fie binare, trebuie să ștergeți tot ceea ce a scris "Găsirea soluțiilor".
Singurele lucruri care necesită modificări aici (cu excepția adăugării termenilor binare în „soluția de căutare“ pentru k-medianele), - un calcul al distanțelor în rândurile 34 la 38. Începeți cu celule M34, în care distanța dintre Adams și centrul grupului 1.
Pentru a număra coincidența tranzacțiilor în Adams și în grupul 1, trebuie să aplicați acestor două coloane SUMPRODUCT / SUMPRODUCTS. Dacă una dintre ele sau ambele este găsit 0, șirul este gol, dar dacă ambii 1, atunci este o coincidență procesată SUMPRODUCT / SUMPRODUCT și 1 înmulțit cu 1 rămâne 1.
În ceea ce privește extragerea rădăcinii din numărul de tranzacții realizate în vector, acesta este pur și simplu SQRT // ROOT suprapus pe SUM // SUM al vectorului. Astfel, ecuația de distanță poate fi scrisă ca
Observați "1-" la începutul formulei, care distinge cosinusul de distanța de cosinus. De asemenea, spre deosebire de distanța euclidiană, distanța de calcul a cosinusului nu necesită folosirea formulelor de matrice.
În orice caz, atunci când îl inserați în M34, ar trebui să adăugați o verificare de eroare în cazul în care centrul clusterului devine 0:
Adăugarea unei formule IFERROR / IFERROR elimină diviziunea de 0. Dacă pentru un motiv oarecare, „găsirea de soluții“, selectează centrul de cluster, complet format din 0, puteți presupune că acest centru se află la o distanță de 1 din restul (1 ca cea mai mare valoarea variabilei binare).
Apoi, puteți copia în jos M34 la coloana M38 și modificați referirile la coloana H I, J, K și L. Ca și în cazul distanței Euclidiene, utilizați referințe absolute ($) în formula, astfel încât să puteți trage undeva fără a lua în considerare coloana cu centrul de cluster.
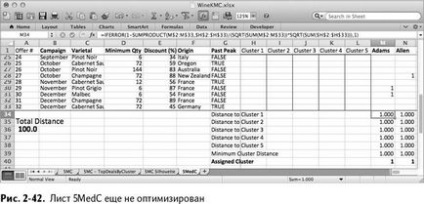
Deci, avem o foaie de 5MedC (Figura 2-42), care este absolut identică cu foaia de 5MS cu care lucram.
Acum, pentru a găsi clustere, deschideți "Căutarea soluției" și schimbați condiția "<= 1» для Н2:L33 на бинарное.
Faceți clic pe Executare. Puteți să vă odihniți timp de o jumătate de oră în timp ce computerul caută clusterele optime pentru dvs. Veți observa imediat că toate centrele de cluster sunt acum binare, astfel încât formatarea condiționată are două nuanțe, ceea ce sporește considerabil contrastul.
Evaluarea tranzacțiilor pentru clustere 5-mediane
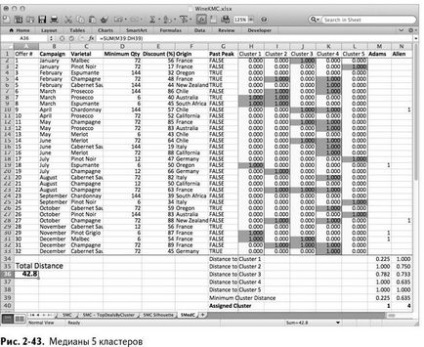
La finalizarea căutării "Căutați o soluție" aveți 5 centre de cluster și în fiecare - o grămadă de unități care indică tranzacțiile preferate de acest grup. Soluțiile mele de găsire au dat o valoare obiectivă optimă de 42,8, deși a ta poate diferi semnificativ (Figura 2-43).
Să analizăm aceste grupuri utilizând metoda de numărare a tranzacțiilor pe care am folosit-o pentru mediile k. Pentru aceasta, copiați mai întâi fila 5MC - fila TopDealsByCluster și numiți-o 5MedC - TopDealsByCluster.
Clusterele dvs. pot diferi ușor de a mea în ordine și în compoziție datorită algoritmului evolutiv, dar sper că diferențele vor fi nesemnificative. Să trecem prin grupuri și să vedem cum acest algoritm a împărțit cumpărătorii.
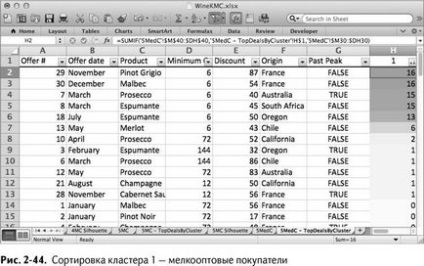
Grupul de sortare 1: se pare că este un cluster cu grupuri mici (Figura 2-44).
Clusterele 2 au fost cumpărate de cumpărători care cumpărău numai vinuri spumante. Șampanie, proză și spumante domină în primele 11 poziții ale clusterului (figura 2-45). Este interesant de observat că abordarea k-mediu nu este foarte clar demonstrată de un grup amator cu k egal cu 4 sau 5.
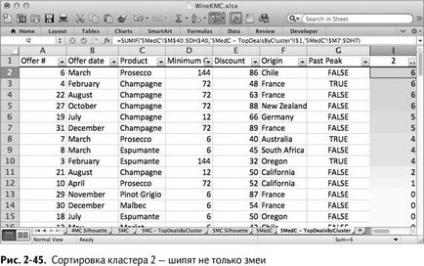
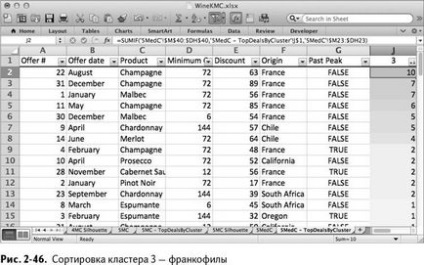
Clusterul 3 este un grup de francofili. Cele mai mari cinci tranzacții sunt pentru vinurile franceze (figurile 2-46). Nu știu că vinurile californiene sunt mai bune?
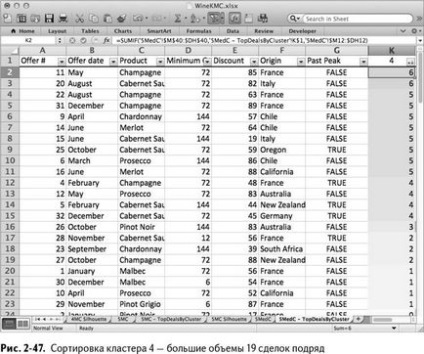
În ceea ce privește clusterul 4, aici sunt doar oferte importante. Și toate cele mai populare oferte - cu un discount mare și care nu au depășit încă prețul maxim (Fig. 2-47).
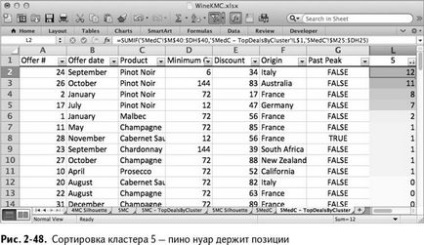
Clusterul 5 a fost din nou un cluster de pinot noir (Figura 2-48).
Deci e mai curat, nu-i așa? Acest lucru se datorează faptului că metoda k-mediană, utilizând metodele asimetrice de măsurare a distanțelor, cum ar fi egalitatea cosinelor, vă permite să grupați clienții pe baza preferințelor lor și nu pe antipatii. La urma urmei, suntem interesați doar de asta!
Asta este capabil de o măsură de distanță!
Acum puteți lua legături la aceste cinci clustere, le puteți importa înapoi în MailChimp.com ca un câmp fuzionat în lista de corespondență și utilizați aceste valori pentru a vă configura corespondența de marketing pentru clustere. Acest lucru ar trebui să vă ajute să luați mai bine cumpărătorii și să gestionați vânzările.