Numărul complex
Exemple de numere complexe conjugate:
Pentru a împărți două numere complexe în formă algebrică, de regulă, este convenabil să se înmulțească numitorul și numitorul fracțiunii cu numărul conjugat la numitor [1, p. 190-191].
Exemplul 4 Efectuați diviziunea:
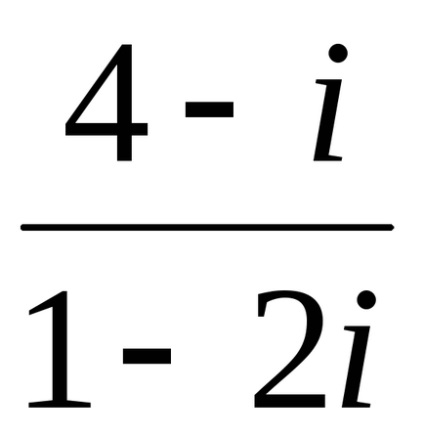
=. Observăm asta
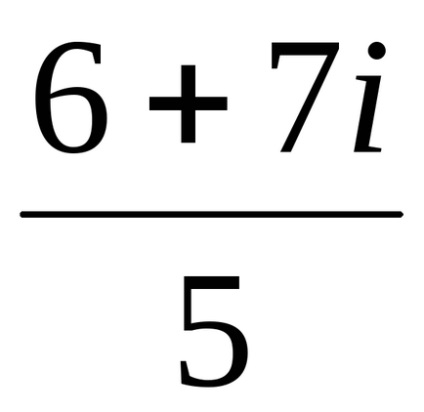
Exemplu 5 Faceți următoarele:
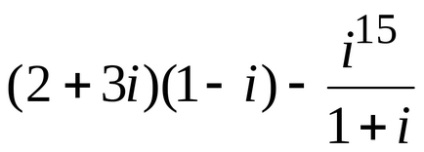
=
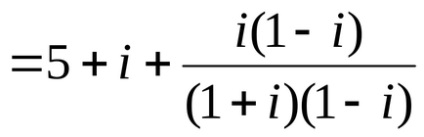
Exemplu 6 Efectuați acțiuni:
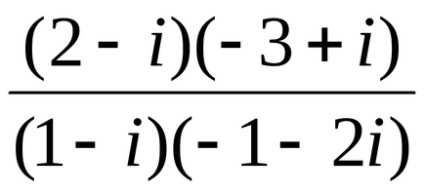
=
=.
Extracția rădăcinii pătrată a unui număr complex în formă algebrică
Definiția. Numărul complex
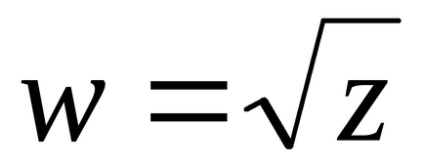
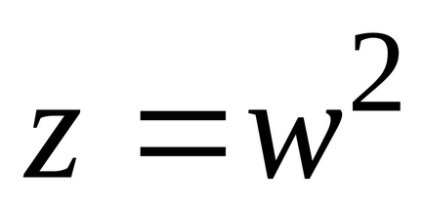
Exemplul 7 Calculați
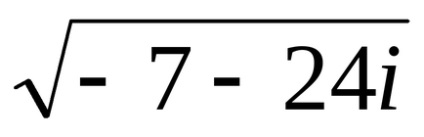
Soluția. lăsa
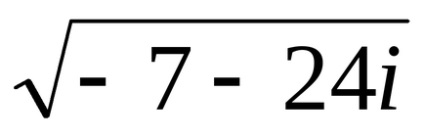
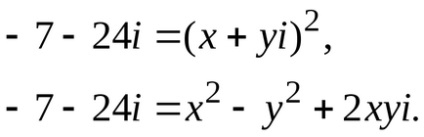
Noi compunem sistemul, echivalând părțile reale și imaginare ale părților stângi și drepte ale ecuației:
Rezolvăm separat ecuația bivadratică:
O altă soluție este posibilă după introducerea formei trigonometrice a numărului complex (vezi pagina 14).
Soluție de ecuații liniare și patrate pentru numere complexe
În regiunea numerelor complexe, aceleași formule pentru soluția ecuațiilor liniare și patrate sunt adevărate ca și în regiunea numerelor reale.
Exemplul 9 Rezolvați ecuația :.
Soluția. Folosim formula pentru găsirea rădăcinilor ecuației patrate:
Exemplul 10 Rezolvați ecuația :.
Exemplul 11 Rezolvați ecuația:

Noi compunem sistemul, echivalând părțile reale și imaginare ale părților stângi și drepte ale ecuației:
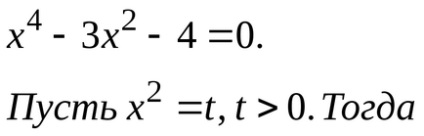
Exemplul 12 Rezolvarea sistemului de ecuații:
Soluția. Exprimăm variabila x din prima ecuație a sistemului în termenii variabilei y:
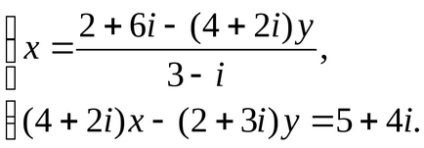
Înmulțim numitorul și numitorul fracțiunii cu numărul conjugat la numitor:
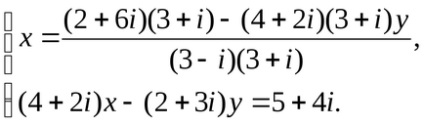
În numerotatorul fracțiunii deschidem parantezele și oferim următorii termeni:
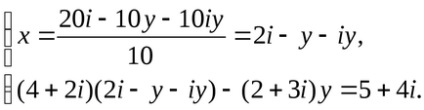
Substituim valoarea obținută a variabilei x în a doua ecuație a sistemului:
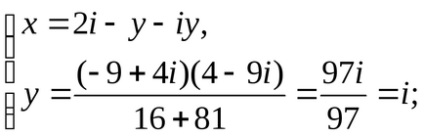
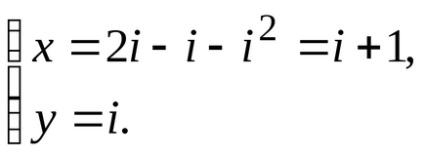
Forma trigonometrică de numere complexe
Reprezentarea geometrică a numerelor complexe
Când studiază proprietățile numerelor complexe, interpretarea lor geometrică este foarte convenabilă [1, p. 186-187]. Deoarece un număr complex este definit ca o pereche de numere reale, fiecare număr complex z = a + bi este reprezentat de un punct al planului (x, y) cu coordonatele x = a și y = b. Un astfel de plan este numit un plan complex. abscisa este axa reală (Rez), iar axa ordonată este axa imaginară (Imz).
Exemplul 13 Desenați în plan punctele corespunzătoare numerelor:
P

Pentru z2, partea reală este 0, iar partea imaginară este 3. Prin urmare, imaginea numărului z2 este punctul (0, 3). Pentru z3, partea reală este 1, iar partea imaginară este -4. Prin urmare, imaginea numărului z3 este punctul (1, -4).
Pentru z4, partea reală este 1 și imaginară 1. Prin urmare, imaginea numărului z4 este punctul (1, 1).
Pentru z5, partea reală este -3 și imaginarul -2. Prin urmare, imaginea numărului z5 este punctul (-3, -2).
Numerele conjugate sunt reprezentate de puncte pe planul complex care sunt simetrice în raport cu axa real Rez.