Astfel, inf și sup sunt definite pentru toate perechile. În consecință, diagrama Hasse luată în considerare este o latură.
Să verificăm dacă rețeaua este modulară, luați în considerare vârfurile 2, 4, 5:
Această grătare nu este distributivă, deoarece nu este modulară.
Desenați o diagramă Hasse a rețelei divizoarelor de numărul 14. Are această latură o algebră booleană? Dacă răspunsul este afirmativ, determinați numărul elementelor sale. Este această algebră universală simplă?
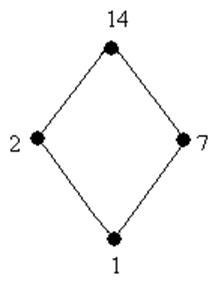
Determinăm dacă latura formează o algebră booleană. Pentru algebra booleană, trebuie îndeplinite următoarele condiții:
1) rețeaua este distributivă,
1) rețeaua este distributivă, deoarece nu conține o sublattică a formei:
Prin urmare, lattica formează o algebră booleană.
Construim structura de congruență prin următorul principiu:
Rețineți că dacă, atunci elementele de la 2 și 7 trebuie să aparțină aceleiași clase, prin urmare, ajungem.
Astfel, rețeaua de congruență are forma:
Pentru ca algebra universală să fie simplă, rețeaua de congruență trebuie să conțină numai elemente extreme. Prin urmare, VA nu este simplu.
Denumiți N = á, * - algebra universală a numerelor naturale cu funcționarea produsului. Luați în considerare elementele 384 și 4374 ale acestei algebre și indicați prin B subalgebra generată de aceste două elemente.
Numărul 60466176 aparține acestei subalgebre?
Extinim numărul de factori:
Descompunerea conține un element mai mic decât cel care formează o subalgebră și, prin urmare, nu îi aparține, de unde numărul 60466176 nu este un element al subalgebrului B.
Luați în considerare grupul de reziduuri Z231 al grupului de aditivi de întregi Z modulo 231.
Determinați structura de congruență a acestui grup.
Este simplu?
-grupa de reziduuri de numere întregi mod 33
Obținem următoarea latură:
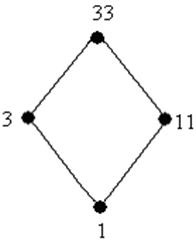
Gridul de congruență (a se vedea Problema 2) are următoarea formă:
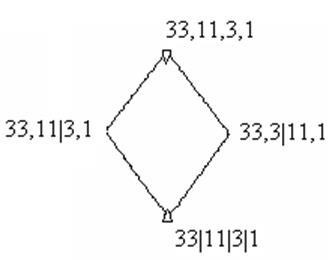
Deoarece latura de congruență, pe lângă elementele extreme, conține și alte elemente, o algebră universală nu este simplă.
Este algebra universală Z231 din problema anterioară direct descompusă?
În consecință, această algebră universală este direct descompusă.
Soiul formează următoarea colecție: grupurile de reziduuri de întregi Zn ca o clasă de algebre universale?
Nu, deoarece axiomul de apartenență al produsului din grupul de reziduuri în clasă nu este deținut.
Ministerul Educației și Științei al Federației Ruse
Departamentul de Algebră și Logică Matematică