Începem prin construirea unui grafic simplu 2-dimensional: complotul păcatului (sqrt (7) x) + 19cos (x) pentru x de la -20 la 20
Dacă înlocuiți 7 (-7), obținem graficele ale părților reale și imaginare ale funcțiilor: complot păcat (sqrt (-7) x) + 19cos (x) pentru x -5-5
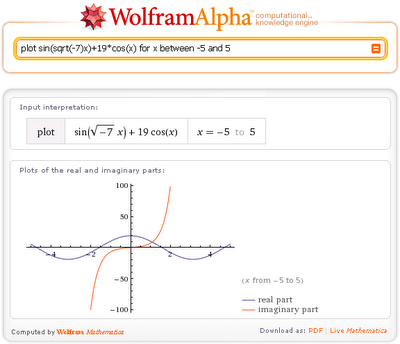
În cele două exemple anterioare, am setat intervalul argumentului x. Și ce se va întâmpla dacă nu specificăm gama de valori ale lui x?
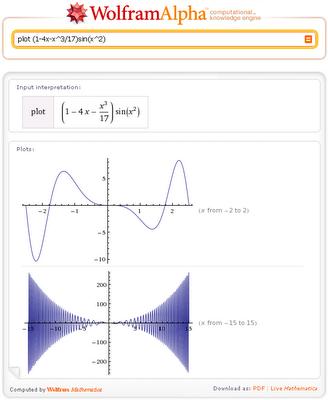
Una dintre trăsăturile unice ale lui Wolfram | Alpha este selectarea automată a intervalului corespunzător funcțiilor grafice x uneia sau a două variabile, de exemplu, prin reprezentarea grafică a acestei funcții care conține funcții Bessel:
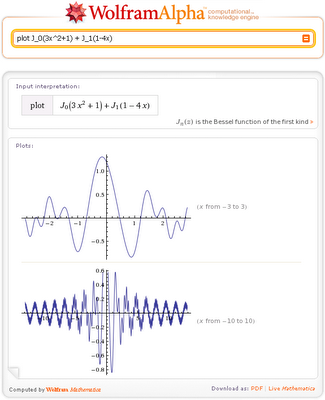
Întorcându-se la Wolfram | Alpha, pentru a construi o funcție de grafic, întotdeauna folosim complotul prefixului. Dacă introducem o expresie unidimensională fără plotarea prefixului. atunci obținem în plus față de funcțiile de grafic în coordonate carteziene dreptunghiulare și multe alte informații despre această funcție.
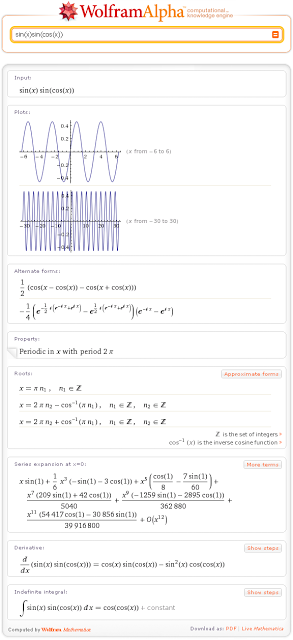
În plus, imaginea graficului construit va fi mai mare dacă utilizați graficul prefixului.
În același timp, în Wolfram | Alpha puteți crea grafică a mai multor funcții.
Acum ia în considerare modul în Wolfram | Alpha construiește grafice ale funcțiilor a două variabile. Începem cu funcția y ^ 2 cos (x) pentru x de la -6 la 6 și y de la -2 la 2
Ca și în cazul unidimensional, Wolfram | Alpha determină automat intervalul corespunzător de valori ale argumentelor, unde funcția are cea mai caracteristică formă. În cazul în care Wolfram | Alpha nu poate găsi o gamă adecvată, este cel mai probabil deoarece sistemul nu a putut determina o astfel de gamă în care funcția are cel mai interesant comportament. În acest caz, putem seta intervalul manual, așa cum sa procedat mai sus. Uitați-vă la următoarele exemple:- compară păcatul (x cos (y))
- plot (x ^ 5-4 aprilie x ^ y ^ 2 + x y - 1) / (y ^ 11 - x ^ 11 + 34 x ^ 3y + 1)
- plot (1 - x) / (2 x + 7, y), 5 x ^ 2 - 3y ^ 2 + 7 xy, (x + 2 y) ^ 4
- complotul sqrt (1 + x y), sqrt (x ^ 2 - y ^ 2 + 2 x y)
- compară păcatul (x + I y)
- complot sqrt (y ^ 2 + 4 y) - sqrt (-I x ^ 3 + 3 x)